

Springer book web pages are here: https://www.springer.com/us/book/9783319781440
Copyright Springer International Publishing 2018-present
Dr Stephen Lynch FIMA SFHEA
# Define the logistic map function - save file as fmu.py.
# Run the Module (or type F5).
"""
You can write your own text here.
Created on Tue Jan 23 09:23:47 2018
@author: sladmin
"""
def fmu(mu, x):
return mu * x * (1 - x)
fmu(3, 0.2)
0.4800000000000001
# Define a function to convert degrees Fahrenheit to Kelvin.
# Save file as F2K.py.
# Run the Module (or type F5).
def F2K():
F = int(input('Enter temperature in degrees Fahrenheit: '))
K = (F + 459.67) * 5 / 9
# Format the output to eight digits with 4 decimal places.
print('Temperature in Kelvin is {:08.4f} K'.format(K))
F2K()
Enter temperature in degrees Fahrenheit: 50 Temperature in Kelvin is 283.1500 K
# Define a function to list the first n terms of the Fibonacci sequence.
# Save file as fibonacci.py.
# Run the Module (or type F5).
def fibonacci(n):
a, b = 0, 1
print(a), print(b), print(a + b)
for i in range(n - 3):
a, b = b, a + b
print(a + b)
fibonacci(10)
0 1 1 2 3 5 8 13 21 34
# Define a function that sums the natural numbers to N.
# Save file as sumN.py.
# Run the Module (or type F5).
def sumN(n):
sum = 0
i = 1
while i <= n:
sum += i
i += 1 # update counter
print('The sum is', sum)
sumN(100)
The sum is 5050
# Euclid's algorithm to find the greatest common divisor.
# See Exercise 10.
# Run the Module (or type F5).
a = 12348
b = 14238
while b != 0:
d = a % b
a = b
b = d
print('The greatest common divisor is {}'.format(a))
The greatest common divisor is 126
# A program to grade student results.
# Run the Module (or type F5).
def grade(score):
if score >= 70:
letter = 'A'
elif score >= 60:
letter = 'B'
elif score >= 50:
letter = 'C'
elif score >= 40:
letter = 'D'
else:
letter = 'F'
return letter
grade(75)
'A'
# Guess the number game.
# Save file as GuessNumber.
# Run the Module (or type F5).
import random # Import the random module.
num_guesses = 0
name = input('Hi! What is your name? ')
number = random.randint(1, 20) # A random integer between 1 and 20.
print('Welcome, {}! I am thinking of an integer between 1 and 20.'.format(name))
while num_guesses < 6:
guess = int(input('Take a guess and type the integer? '))
num_guesses += 1
if guess < number:
print('Your guess is too low.')
if guess > number:
print('Your guess is too high.')
if guess == number:
break
if guess == number:
print('Well done {}! You guessed my number in {} guesses!'.format(name, num_guesses))
else:
print('Sorry, you lose! The number I was thinking of was {}'.format(number))
Hi! What is your name? Stephen Welcome, Stephen! I am thinking of an integer between 1 and 20. Take a guess and type the integer? 10 Your guess is too low. Take a guess and type the integer? 15 Your guess is too low. Take a guess and type the integer? 18 Your guess is too high. Take a guess and type the integer? 16 Your guess is too low. Take a guess and type the integer? 17 Well done Stephen! You guessed my number in 5 guesses!
# Cantor fractal set.
# To be run in IDLE.
# Run Module and type >>> cantor(-200, 200, 300) in Python Shell.
# Run the Module (or type F5).
from turtle import *
def cantor(x, y, length):
if length >= 5: # Exit program if length < 5.
penup() # Raise the turtle.
pensize(3) # Line thickness.
pencolor('blue')
setpos(x , y) # Coordinates of start point.
pendown() # Put turtle down.
fd(length) # Forward.
y -= 30 # y = y - 30.
cantor(x , y, length / 3)
cantor(x + 2 * length / 3, y, length / 3)
penup()
setpos(x , y + 30)
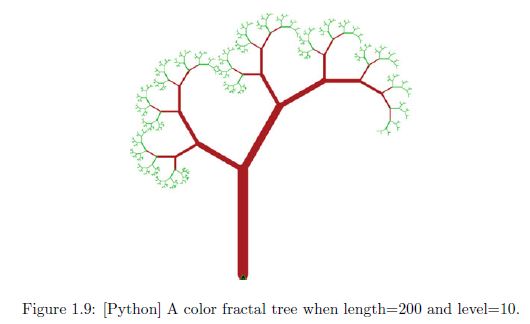
# To be run in IDLE.
# A program to plot a color fractal tree.
# Run Module and type >>> FractalTreeColor(200,10) in Python Shell.
# Run the Module (or type F5).
from turtle import *
setheading(90) # The turtle points straight up.
penup() # Lift the pen.
setpos(0,-250) # Set initial point.
pendown() # Pen down.
def FractalTreeColor(length, level):
"""
Draws a fractal tree
"""
pensize(length/10) # Thickness of lines.
if length < 20:
pencolor("green")
else:
pencolor("brown")
speed(0)
if level > 0:
fd(length) # Forward.
rt(30) # Right turn 30 degrees.
FractalTreeColor(length*0.7, level-1)
lt(90) # Left turn 90 degrees.
FractalTreeColor(length*0.5, level-1)
rt(60) # Right turn 60 degrees.
penup()
bk(length) # Backward.
pendown()
FractalTreeColor(200,10)
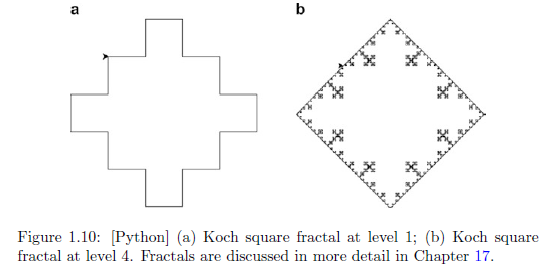
# Koch square fractal.
# Run the Module (or type F5).
from turtle import *
def KochSquare(length, level): # KochSquare function.
speed(0) # Fastest speed.
for i in range(4):
PlotSide(length, level)
rt(90)
def PlotSide(length, level): # PlotSide function.
if level==0:
fd(length)
return
PlotSide(length/3, level-1)
lt(90)
PlotSide(length/3 ,level-1)
rt(90)
PlotSide(length/3, level-1)
rt(90)
PlotSide(length/3, level-1)
lt(90)
PlotSide(length/3, level-1)
KochSquare(200,4)
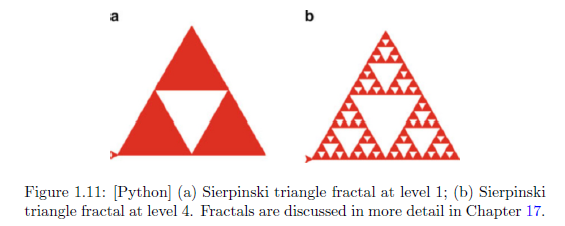
# Sierpinski triangle.
# See Figure 1.11.
# Run the Module (or type F5).
from turtle import *
def Sierpinski(length, level): # Function.
speed(0) # Fastest speed.
if level==0:
return
begin_fill() # Fill shape.
color("red")
for i in range(3):
Sierpinski(length/2, level-1)
fd(length)
lt(120) # Left turn 120 degrees.
end_fill()
Sierpinski(200,5)

# Program 01a: A program that solves a simple Ordinary Differential Equation (ODE).
# See Example 10.
from sympy import dsolve, Eq, symbols, Function
t=symbols('t')
x=symbols('x',cls=Function)
deqn1=Eq(x(t).diff(t),1-x(t))
sol1=dsolve(deqn1,x(t))
print(sol1)
Eq(x(t), C1*exp(-t) + 1)
# Program 01b: A program that solves a second order ODE.
from sympy import Function, Eq, dsolve, symbols, exp
t=symbols('t')
y=symbols('y',cls=Function)
deqn2=Eq(y(t).diff(t,t) + y(t).diff(t) + y(t), exp(t))
sol2 = dsolve(deqn2, y(t))
print(sol2)
Eq(y(t), (C1*sin(sqrt(3)*t/2) + C2*cos(sqrt(3)*t/2))*exp(-t/2) + exp(t)/3)
# Program 01c: Two curves on one plot.
# See Figure 1.14.
import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 2.0, 0.01)
c=1+np.cos(2*np.pi*t)
s = 1 + np.sin(2*np.pi*t)
plt.plot(t,s,'r--',t,c,'b-.')
plt.xlabel('time (s)')
plt.ylabel('voltage (mV)')
plt.title('Voltage-time plot')
plt.grid(True)
plt.savefig("Voltage-Time Plot.png")
plt.show()
# Program 01d: Subplots.
# See Figure 1.15.
import matplotlib.pyplot as plt
import numpy as np
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
t1=np.arange(0.0, 5.0, 0.1)
t2=np.arange(0.0, 5.0, 0.02)
plt.figure(1)
plt.subplot(211) #subplot(num rows,num cols,fig num)
plt.plot(t1,f(t1),'bo',t2,f(t2),'k',label='damping')
plt.xlabel('time (s)')
plt.ylabel('amplitude (m)')
plt.title('Damped pendulum')
legend = plt.legend(loc='upper center',shadow=True)
plt.subplot(212)
plt.plot(t2, np.cos(2*np.pi*t2),'g--',linewidth=4)
plt.xlabel('time (s)')
plt.ylabel('amplitude (m)')
plt.title('Undamped pendulum')
plt.subplots_adjust(hspace=0.8)
plt.show()
# Program 01e: Surface and contour plots.
# See Figure 1.16.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
alpha=0.7
phi_ext=2*np.pi*0.5
def flux_qubit_potential(phi_m,phi_p):
return 2+alpha-2*np.cos(phi_p)*np.cos(phi_m)-alpha*np.cos(phi_ext-2*phi_p)
phi_m=np.linspace(0,2*np.pi,100)
phi_p=np.linspace(0,2*np.pi,100)
X,Y=np.meshgrid(phi_p,phi_m)
Z=flux_qubit_potential(X,Y).T
fig=plt.figure(figsize=(8,6))
ax=fig.add_subplot(1,1,1,projection='3d')
p=ax.plot_wireframe(X, Y, Z, rstride=4, cstride=4)
ax.plot_surface(X,Y,Z,rstride=4,cstride=4,alpha=0.25)
cset=ax.contour(X,Y,Z,zdir='z',offset=-np.pi,cmap=plt.cm.coolwarm)
cset=ax.contour(X,Y,Z,zdir='x',offset=-np.pi,cmap=plt.cm.coolwarm)
cset=ax.contour(X,Y,Z,zdir='y',offset=3*np.pi,cmap=plt.cm.coolwarm)
ax.set_xlim3d(-np.pi, 2*np.pi);
ax.set_ylim3d(0, 3*np.pi);
ax.set_zlim3d(-np.pi, 2*np.pi);
ax.set_xlabel('$\phi_p$',fontsize=15)
ax.set_ylabel('$\phi_m$',fontsize=15)
ax.set_zlabel('Potential',fontsize=15)
plt.tick_params(labelsize=15)
ax.set_title("Surface and contour plots",fontsize=15)
plt.show()
# Program 01f: Parametric curve in 3D.
# See Figure 1.17.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(8,6))
ax=fig.add_subplot(1,1,1,projection='3d')
t = np.linspace(-10,10,1000)
x = np.sin(t)
y = np.cos(t)
z = t
ax.plot(x, y, z)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("3D Parametric Curve")
plt.show()
# Program 01g: Animation of a simple curve.
# Hit the green play button (Run file (F5)).
# Run %matplotlib qt5 in IPython console before animating.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
fig = plt.figure()
ax = plt.axes(xlim=(0, 2),ylim=(-2, 2))
line, = ax.plot([],[],lw=2)
plt.xlabel('time')
plt.ylabel('sin($\omega$t)')
plt.close()
def init():
line.set_data([],[])
return line,
# The function to animate.
def animate(i):
x = np.linspace(0, 2, 1000)
y = np.sin(2*np.pi*(0.1*x*i))
line.set_data(x, y)
return line,
# Note: blit=True means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, init_func=init, \
frames=100, interval=200, blit=False)
from IPython.display import HTML
HTML(anim.to_jshtml())
# Program 02a: A separable ODE.
from sympy import *
t=symbols('t')
x=symbols('x',cls=Function)
sol=dsolve(Eq(x(t).diff(t), -t/x(t)), x(t))
print(sol)
[Eq(x(t), -sqrt(C1 - t**2)), Eq(x(t), sqrt(C1 - t**2))]
# Program 02b: The logistic ODE.
from sympy import *
t=symbols('t'); a=symbols('a'); b=symbols('b')
P=symbols('P',cls=Function)
sol=dsolve(Eq(P(t).diff(t), P(t)*(a-b*P(t))), P(t))
print(sol)
Eq(P(t), a*exp(a*(C1 + t))/(b*(exp(a*(C1 + t)) - 1)))
# Program 02c : Power series solution of first order ODE.
# See Example 7.
from sympy import dsolve, Function, pprint
from sympy.abc import t
x=Function("x")
ODE1=x(t).diff(t) + t*x(t) - t**3
pprint(dsolve(ODE1, hint='1st_power_series', n = 8, ics = {x(0):1}))
2 4 6
t 3⋅t t ⎛ 8⎞
x(t) = 1 - ── + ──── - ── + O⎝t ⎠
2 8 16
# Program 02d : Power series solution of second order ODE.
# See Example 8.
from sympy import dsolve, Function, pprint
from sympy.abc import t
x=Function("x")
ODE2=x(t).diff(t,2) + t**2*x(t).diff(t) - x(t)
pprint(dsolve(ODE2,hint = '2nd_power_series_ordinary', n=6))
⎛ 4 2 ⎞ ⎛ 3 2 ⎞
⎜t t ⎟ ⎜ t t ⎟ ⎛ 6⎞
x(t) = C₂⋅⎜── + ── + 1⎟ + C₁⋅t⋅⎜- ── + ── + 1⎟ + O⎝t ⎠
⎝24 2 ⎠ ⎝ 12 6 ⎠
# Program 02e: Numerical and truncated series solutions.
# See Figure 2.6.
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import numpy as np
def ODE2(X, t):
x = X[0]
y = X[1]
dxdt = y
dydt = x - t**2*y
return [dxdt, dydt]
X0 = [1, 0]
t = np.linspace(0, 10, 1000)
sol = odeint(ODE2, X0, t)
x = sol[:, 0]
y = sol[:, 1]
fig, ax = plt.subplots()
ax.plot(t,x,label='Numerical')
ax.plot(t, 1 + t**2/2 + t**4/24,'r-', label='Truncated series')
plt.xlabel("t",fontsize=15)
plt.ylabel("x",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(0,4)
plt.ylim(0,4)
legend = ax.legend(loc='lower center', shadow=True)
plt.show()
# Program 2f: A linear first order ODE.
from sympy import Function, dsolve, Eq, symbols, sin
t=symbols('t');
I=symbols('I', cls=Function)
sol=dsolve(Eq(I(t).diff(t), 5*sin(t) - I(t)/5), I(t))
print(sol)
Eq(I(t), (C1 + 25*exp(t/5)*sin(t)/26 - 125*exp(t/5)*cos(t)/26)*exp(-t/5))
# Program 02g: A second order ODE.
from sympy import symbols, dsolve, Function,Eq, sin
t=symbols('t');
I=symbols('I', cls=Function)
sol=dsolve(Eq(I(t).diff(t,t) + 5*I(t).diff(t) + 6*I(t), 10*sin(t)), I(t))
print(sol)
Eq(I(t), C1*exp(-3*t) + C2*exp(-2*t) + sin(t) - cos(t))
# Program 02h: Chemical kinetics - conservation of mass.
# See Exercise 7, the reaction: A -> B -> C.
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Set parameters and initial conditions
r1, r2 = 0.01, 0.02
x0, y0, z0 = 1000, 0, 0
# Maximum time point and total number of time points
tmax, n = 500, 10000
def Chemical_Kinetics(X, t, r1, r2):
#The Differential Equations
x, y, z = X
dx = -r1 * x
dy = r1 * x - r2 * y
dz = r2 * y
return (dx, dy, dz)
# Integrate differential equations on the time grid t.
t = np.linspace(0, tmax, n)
f = odeint(Chemical_Kinetics, (x0, y0, z0), t, args=(r1, r2))
x, y, z = f.T
plt.figure(1)
plt.xlabel('Time')
plt.ylabel('Concentrations')
plt.title('Chemical Kinetics')
plt.plot(t, x, label='|A|')
plt.plot(t, y, label='|B|')
plt.plot(t, z, label='|C|')
legend = plt.legend(loc='best')
plt.show()
# Program 03a: Phase portrait of a linear system.
# See Figure 3.8(a).
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
import pylab as pl
# The 2-dimensional linear system.
a, b, c, d = 2, 1, 1, 2
def dx_dt(x, t):
return [a*x[0] + b *x[1], c*x[0] + d*x[1]]
# Trajectories in forward time.
ts = np.linspace(0, 4, 100)
ic = np.linspace(-1, 1, 5)
for r in ic:
for s in ic:
x0 = [r, s]
xs = odeint(dx_dt, x0, ts)
plt.plot(xs[:,0], xs[:,1], "r-")
# Trajectories in backward time.
ts = np.linspace(0, -4, 100)
ic = np.linspace(-1, 1, 5)
for r in ic:
for s in ic:
x0 = [r, s]
xs = odeint(dx_dt, x0, ts)
plt.plot(xs[:,0], xs[:,1], "r-")
# Label the axes and set fontsizes.
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(-1,1)
plt.ylim(-1,1)
# Plot the vectorfield. See lines 10, 12 for system.
X,Y = np.mgrid[-1:1:10j,-1:1:10j]
u=a*X + b*Y
v=c*X + d*Y
pl.quiver(X,Y,u,v, color='b')
plt.show()
# Program 03b: Nonlinear system, phase portrait with vector plot.
# See Figure 3.12.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
import pylab as pl
# The 2-dimensional nonlinear system.
def dx_dt(x, t):
return [x[1], x[0]*(1-x[0]**2) + x[1]]
# Trajectories in forward time.
ts = np.linspace(0, 10, 500)
ic = np.linspace(-3, 3, 6)
for r in ic:
for s in ic:
x0 = [r, s]
xs = odeint(dx_dt, x0, ts)
plt.plot(xs[:,0], xs[:,1], "r-")
# Trajectories in backward time.
ts = np.linspace(0, -10, 500)
ic = np.linspace(-3, 3, 6)
for r in ic:
for s in ic:
x0 = [r, s]
xs = odeint(dx_dt, x0, ts)
plt.plot(xs[:,0], xs[:,1], "r-")
# Label the axes and set fontsizes.
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(-3,3)
plt.ylim(-3,3);
# Plot the vectorfield.
X,Y=np.mgrid[-3:3:20j, -3:3:20j]
u=Y
v=X*(1 - X**2) + Y
pl.quiver(X, Y, u, v, color='b')
plt.show()
# Program 03c: Finding critical points. Check by plotting the curves of intersection.
# See Example 9.
import sympy as sm
x, y = sm.symbols('x, y')
P = x*(1 - x/2 - y)
Q = y*(x - 1 - y/2)
# Set P(x,y)=0 and Q(x,y)=0.
Peqn = sm.Eq(P, 0)
Qeqn = sm.Eq(Q, 0)
# Locate critical points.
criticalpoints = sm.solve((Peqn, Qeqn), x, y)
print(criticalpoints)
[(0, -2), (0, 0), (6/5, 2/5), (2, 0)]
# Program 04a: Holling-Tanner model. See Figures 4.5 and 4.6.
# Time series and phase portrait for a predator-prey system.
# An isolated periodic solution (limit cycle).
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
# The Holling-Tanner model.
def Holling_Tanner(X, t=0):
# here X[0] = x and X[1] = y
return np.array([ X[0]*(1-X[0]/7)-6*X[0]*X[1]/(7+7*X[0]), 0.2*X[1]*(1-0.5*X[1]/X[0]) ])
t = np.linspace(0, 200, 1000)
# initial values: x0 = 7, y0 = 0.1
Sys0 = np.array([7, 0.1])
X, infodict = integrate.odeint(Holling_Tanner,Sys0,t,full_output=True)
x,y = X.T
fig = plt.figure(figsize=(15,5))
fig.subplots_adjust(wspace = 0.5, hspace = 0.3)
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.plot(t,x, 'r-',label='prey')
ax1.plot(t,y, 'b-',label='predator')
ax1.set_title("Time Series")
ax1.set_xlabel("time")
ax1.grid()
ax1.legend(loc='best')
ax2.plot(x, y, color="blue")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.set_title("Phase portrait")
ax2.grid()
plt.show()
# Program 04b: Predator-prey phase portrait.
# See Exercise 5(a): Co-existence of species at a single critical point.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
import pylab as pl
def dx_dt(x, t):
return [x[0]*(4-x[1]-x[0]), x[1]*(3*x[0]-1-x[1])]
ts = np.linspace(0, 20, 500)
xs = odeint(dx_dt, [4,0.01], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-')
xs = odeint(dx_dt, [0.5,7], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-')
xs = odeint(dx_dt, [0.01,0], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-',linewidth=3)
xs = odeint(dx_dt, [6,2], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-')
xs = odeint(dx_dt, [0,7], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-',linewidth=3)
xs = odeint(dx_dt, [6,0], ts)
plt.plot(xs[:, 0], xs[:, 1], 'r-',linewidth=3)
# Label the axes and set fontsizes.
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(0, 6)
plt.ylim(0, 7)
# Plot the vectorfield.
X, Y = np.mgrid[0:6:10j, 0:7:10j]
u = X*(4-X-Y)
v = Y*(3*X-1-Y)
pl.quiver(X, Y, u, v, color='b')
plt.show()
# Program 05a: Limit cycle for Fitzhugh-Nagumo.
# See Figure 5.3.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
theta=0.14;omega=0.112;gamma=2.54;epsilon=0.01;
xmin=-0.5;xmax=1.5;ymin=0;ymax=0.3;
def dx_dt(x, t):
return [-x[0]*(x[0]-theta)*(x[0]-1)-x[1]+omega, epsilon*(x[0]-gamma*x[1])]
# Trajectories in forward time.
xs=odeint(dx_dt,[0.5,0.09],np.linspace(0,100,1000))
plt.plot(xs[:,0],xs[:,1], "r-")
# Label the axes and set fontsizes.
plt.xlabel("u",fontsize=15)
plt.ylabel("v",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(xmin,xmax)
plt.ylim(ymin,ymax);
# Plot the nullclines where dx/dt and dy/dt are zero.
x=np.arange(xmin,xmax,0.01)
plt.plot(x, x/gamma, 'b--', x, -x*(x-theta)*(x-1)+omega,'b--')
plt.show()
# Program 05b: Example 7, approximate solutions.
# See Figure 5.9.
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import numpy as np
eps=0.3
def ODE(x, t):
return eps*x**2 - x
x0 = 2
t = np.linspace(0, 10, 1000)
sol = odeint(ODE, x0, t)
x = np.array(sol).flatten()
plt.plot(t,x,label='x(t)')
plt.plot(t,2*np.exp(-t),label='O(1)')
plt.plot(t,2*np.exp(-t)+4*eps*(np.exp(-t)-np.exp(-2*t)),label='O($\epsilon $)')
plt.plot(t,2*np.exp(-t)+4*eps*(np.exp(-t)-np.exp(-2*t))+ \
eps**2*8*(np.exp(-t)-2*np.exp(-2*t)+np.exp(-3*t)),label='O($\epsilon^2$)')
plt.xlabel('t', fontsize=15)
plt.ylabel('x', fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(0, 8)
plt.ylim(0, 2.1)
plt.legend()
plt.show()
# Program 05c: Error between xN and x0. See Figure 5.9.
# Error between one term solution and numerical solution.
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import numpy as np
def dx_dt(x,t):
return [x[1], 0.01*x[0]**3 - x[0]]
x0=[1,0]
ts=np.linspace(0,100,2000)
xs=odeint(dx_dt,x0,ts)
xN=xs[:,0]
xpert0=np.cos(ts)
plt.plot(ts,xN-xpert0)
plt.xlabel('t')
plt.ylabel('$x_N-x_0$')
plt.show()
# Program 05d: The Lindstedt-Poincare Method
# Deriving the order epsilon equations.
# See Example 9.
from sympy import collect,expand, Function, Symbol
x0=Function('x0');x1=Function('x1');x2=Function('x2');
x=Function('x')
t=Symbol('t');eps=Symbol('eps');
w1=Symbol('w1');w2=Symbol('w2');
x=x0(t) + eps*x1(t) + eps**2*x2(t)
expr=(1 + eps*w1 + eps**2*w2)**2*x.diff(t,t) + x - eps*x**3
expr=expand(expr)
expr=collect(expr,eps)
print(expr)
-eps**7*x2(t)**3 + eps**6*(w2**2*Derivative(x2(t), (t, 2)) - 3*x1(t)*x2(t)**2) + eps**5*(2*w1*w2*Derivative(x2(t), (t, 2)) + w2**2*Derivative(x1(t), (t, 2)) - 3*x0(t)*x2(t)**2 - 3*x1(t)**2*x2(t)) + eps**4*(w1**2*Derivative(x2(t), (t, 2)) + 2*w1*w2*Derivative(x1(t), (t, 2)) + w2**2*Derivative(x0(t), (t, 2)) + 2*w2*Derivative(x2(t), (t, 2)) - 6*x0(t)*x1(t)*x2(t) - x1(t)**3) + eps**3*(w1**2*Derivative(x1(t), (t, 2)) + 2*w1*w2*Derivative(x0(t), (t, 2)) + 2*w1*Derivative(x2(t), (t, 2)) + 2*w2*Derivative(x1(t), (t, 2)) - 3*x0(t)**2*x2(t) - 3*x0(t)*x1(t)**2) + eps**2*(w1**2*Derivative(x0(t), (t, 2)) + 2*w1*Derivative(x1(t), (t, 2)) + 2*w2*Derivative(x0(t), (t, 2)) - 3*x0(t)**2*x1(t) + x2(t) + Derivative(x2(t), (t, 2))) + eps*(2*w1*Derivative(x0(t), (t, 2)) - x0(t)**3 + x1(t) + Derivative(x1(t), (t, 2))) + x0(t) + Derivative(x0(t), (t, 2))
# Program 06a: Contour plot. See Figure 6.2(a).
import numpy as np
import matplotlib.pyplot as plt
xlist = np.linspace(-10.0,10.0, 100)
ylist = np.linspace(-4.0, 4.0, 100)
X, Y = np.meshgrid(xlist, ylist)
Z = Y**2/2 - 5*np.cos(X)
plt.figure()
plt.contour(X,Y,Z)
plt.xlabel(r'$\theta$',fontsize=20)
plt.ylabel(r'$\phi$',fontsize=20)
plt.tick_params(labelsize=20)
plt.show()
# Program 06b: Surface plot of Hamiltonian. See Figure 6.2(b).
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
def fun(x, y):
return y**2/2 - 5*np.cos(x)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = np.arange(-10.0, 10.0, 0.1)
y = np.arange(-4.0, 4.0, 0.1)
X, Y = np.meshgrid(x, y)
zs = np.array([fun(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
ax.plot_surface(X, Y, Z)
ax.set_xlabel(r'$\theta$',fontsize=12)
ax.set_ylabel(r'$\phi$',fontsize=12)
ax.set_zlabel(r'$H(\theta,\phi)$',fontsize=12)
plt.tick_params(labelsize=12)
ax.view_init(30, -70)
plt.show()
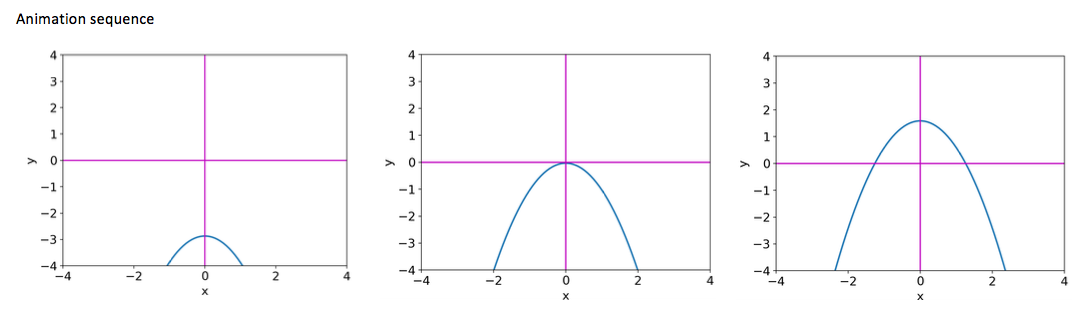
# Program 07a: Animation of a simple curve. Saddle-node bifurcation.
# See Figure 7.2.
# Animation of mu-x**2, as mu increases from mu=-3 to mu=3.
# Type - %matplotlib qt5 - in Console window.
%matplotlib notebook
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
# Set up the figure.
fig=plt.figure()
xmin, xmax, mu_min, mu_max = -4, 4, -3, 3
ax=plt.axes(xlim=(xmin,xmax),ylim=(xmin,xmax))
ax.plot([xmin,xmax],[0,0],'m')
ax.plot([0,0],[xmin,xmax],'m')
line,=ax.plot([],[],lw=2)
def init():
line.set_data([],[])
return line,
# Animate mu-x^**2, where -3<mu<3.
def animate(mu):
x = np.linspace(xmin,xmax,100)
y = mu-x**2
line.set_data(x, y)
return line,
bifurcation=animation.FuncAnimation(fig,animate,init_func=init,
frames=np.linspace(mu_min,mu_max,1000),interval=10,blit=False)
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())
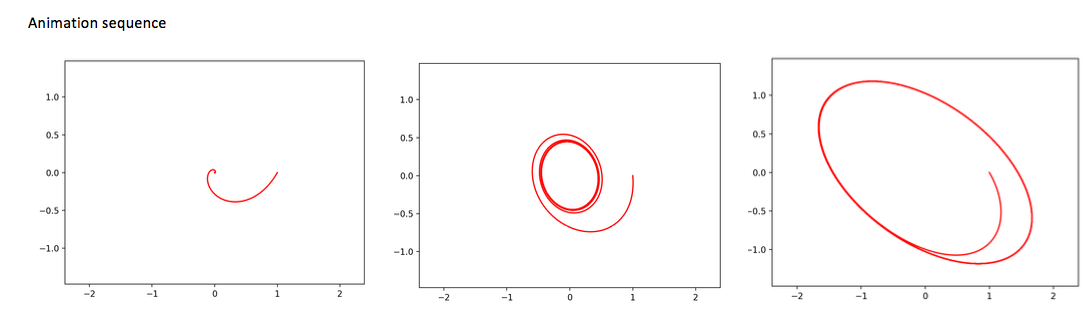
# Program 07b.py. Animation.
# Hopf Bifurcation of a limit cycle from a critical point.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
fig=plt.figure()
myimages=[]
def Hopf(x, t):
return [x[1]+mu*x[0]-x[0]*x[1]**2, mu*x[1]-x[0]-x[1]**3]
time = np.arange(0, 200, 0.01)
x0=[1,0]
for mu in np.arange(-1, 1, 0.1):
xs = odeint(Hopf, x0, time)
imgplot = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot)
my_anim = animation.ArtistAnimation(fig,myimages,interval=100,blit=False,repeat_delay=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())
# Program 07c: Animation of a Saddle Node on an Invariant Circle (SNIC) bifurcation.
# See Figure 7.12.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
fig=plt.figure()
myimages=[]
def SNIC(x, t):
return [x[0]*(1-x[0]**2-x[1]**2)-x[1]*(1+mu+x[0]),
x[1]*(1-x[0]**2-x[1]**2)+x[0]*(1+mu+x[0])]
time = np.arange(0, 200, 0.01)
x0=[0.5,0]
for mu in np.arange(-3, 1, 0.1):
xs = odeint(SNIC, x0, time)
imgplot = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot)
my_anim = animation.ArtistAnimation(fig,myimages,interval=100,blit=False,repeat_delay=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())
# Program 08a: The Rossler chaotic attractor. See Fig. 8.10(a).
# In this case, iteration is used to solve the ODEs.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def Rossler(x,y,z,a=0.2,b=0.2,c=6.3):
x_dot = - y - z
y_dot = x + a*y
z_dot = b + x*z - c*z
return x_dot, y_dot, z_dot
dt = 0.01
stepCnt = 50000
xs=np.empty((stepCnt+1,))
ys=np.empty((stepCnt+1,))
zs=np.empty((stepCnt+1,))
# The initial conditions.
xs[0],ys[0],zs[0] = (1.0,1.0,1.0)
# Iterate.
for i in range(stepCnt):
x_dot,y_dot,z_dot = Rossler(xs[i],ys[i],zs[i])
xs[i+1]=xs[i] + (x_dot*dt)
ys[i+1]=ys[i] + (y_dot*dt)
zs[i+1] =zs[i] + (z_dot*dt)
fig=plt.figure()
ax=Axes3D(fig)
ax.plot(xs, ys, zs, lw=0.5)
ax.set_xlabel("x", fontsize=15)
ax.set_ylabel("y", fontsize=15)
ax.set_zlabel("z", fontsize=15)
plt.tick_params(labelsize=15)
ax.set_title("Rossler Attractor", fontsize=15)
plt.show()
# Program 08b: The Lorenz attractor. See Figure 8.11.
# In this case, the odeint numerical solver was used to solve the ODE.
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Lorenz paramters and initial conditions
sigma, beta, rho = 10, 2.667, 28
x0, y0, z0 = 0, 1, 1.05
# Maximum time point and total number of time points
tmax, n = 100, 10000
def Lorenz(X, t, sigma, beta, rho):
"""The Lorenz equations."""
x, y, z = X
dx = -sigma*(x - y)
dy = rho*x - y - x*z
dz = -beta*z + x*y
return dx, dy, dz
# Integrate the Lorenz equations on the time grid t.
t = np.linspace(0, tmax, n)
f = odeint(Lorenz, (x0, y0, z0), t, args=(sigma, beta, rho))
x, y, z = f.T
# Plot the Lorenz attractor using a Matplotlib 3D projection.
fig=plt.figure()
ax = Axes3D(fig)
ax.plot(x, y, z,'b-',lw=0.5)
ax.set_xlabel("x", fontsize=15)
ax.set_ylabel("y", fontsize=15)
ax.set_zlabel("z", fontsize=15)
plt.tick_params(labelsize=15)
ax.set_title("Lorenz Attractor", fontsize=15)
plt.show()
# Program 08c: The Belousov-Zhabotinski Reaction. See Figure 8.16.
# Plotting time series for a 3-dimensional ODE.
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# B_Z parameters and initial conditions.
q, f, eps, delta = 3.1746e-5, 1, 0.0099, 2.4802e-5
x0, y0, z0 = 0, 0, 0.1
# Maximum time point and total number of time points.
tmax, n = 50, 10000
def B_ZReaction(X,t,q,f,eps,delta):
x, y, z = X
dx = (q*y - x*y + x*(1 - x))/eps
dy = ( - q*y - x*y + f*z)/delta
dz = x - z
return dx, dy, dz
t = np.linspace(0, tmax, n)
f = odeint(B_ZReaction, (x0, y0, z0), t, args=((q,f,eps,delta)))
x, y, z = f.T
# Plot time series.
fig = plt.figure(figsize=(10,3))
fig.subplots_adjust(wspace = 0.5, hspace = 0.3)
ax1 = fig.add_subplot(1,3,1)
ax1.set_title("Relative concentration bromous acid", fontsize=10)
ax2 = fig.add_subplot(1,3,2)
ax2.set_title("Relative concentration bromide ions", fontsize=10)
ax3 = fig.add_subplot(1,3,3)
ax3.set_title("Relative concentration cerium ions", fontsize=10)
ax1.plot(t, x, 'b-')
ax2.plot(t, y, 'r-')
ax3.plot(t, z, 'm-')
plt.show()
# Programs 08d: Animation of a Chua circuit bifurcation.
# You can watch a YouTube animation of a physical circuit on the web.
# Search for Chua circuit animated bifurcation.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
fig=plt.figure()
myimages=[]
mo=-1/7;m1=2/7;Tmax=100;
def Chua(x, t):
return [a*(x[1]-(m1*x[0]+(mo-m1)/2*(np.abs(x[0]+1)-np.abs(x[0]-1)))),x[0]-x[1]+x[2],-15*x[1]]
time = np.arange(0, Tmax, 0.1)
x0=[1.96,-0.0519,-3.077]
for a in np.arange(8, 11, 0.1):
xs = odeint(Chua, x0, time)
imgplot = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot)
anim=animation.ArtistAnimation(fig,myimages,interval=500,\
blit=False,repeat_delay=500)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())

# Program 09a: Poincare first return map.
# See Figure 9.2.
import matplotlib.pyplot as plt
from sympy import sqrt
import numpy as np
from scipy.integrate import odeint
xmin=-1;xmax=1;ymin=-1;ymax=1;
def dx_dt(x, t):
return [-x[1]-x[0]*sqrt(x[0]**2+x[1]**2),x[0]-x[1]*sqrt(x[0]**2+x[1]**2)]
# Phase portrait.
t=np.linspace(0,16*np.pi,10000)
xs=odeint(dx_dt,[1,0],t)
plt.plot(xs[:,0],xs[:,1], "r-")
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(xmin,xmax)
plt.ylim(ymin,ymax);
plt.show()
# First eight returns on x-axis.
t=np.linspace(0,9*2*np.pi,900000)
xs=odeint(dx_dt,[1,0],t)
for i in range(9):
print('r_',i,'=',xs[100000*i,0])
r_ 0 = 1.0 r_ 1 = 0.13730247618333363 r_ 2 = 0.0737116398245952 r_ 3 = 0.050378946444256625 r_ 4 = 0.03826617811397822 r_ 5 = 0.03084905202922912 r_ 6 = 0.02584041437408372 r_ 7 = 0.022231002965186188 r_ 8 = 0.019506343238878496
# Program 09b: Hamiltonian with two degrees of freedom.
# See Figure 9.5(e): quasiperiodic behavior.
import numpy as np
from scipy.integrate import odeint
from sympy import sqrt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Maximum time point and total number of time points
tmax, n = 100, 20000
w1=sqrt(2);w2=1;
def Hamiltonian4D(X, t):
"""Hamiltonian equations."""
p1, p2, q1, q2 = X
dp1 = -w1*q1
dp2 = -w2*q2
dq1 = w1*p1
dq2 = w2*p2
return dp1, dp2, dq1, dq2
t = np.linspace(0, tmax, n)
f = odeint(Hamiltonian4D, (0.5, 1.5, 0.5, 0), t)
p1, p2, q1, q2 = f.T
fig=plt.figure()
ax = Axes3D(fig)
ax.plot(p1, q1, q2,'b-',lw=0.5)
ax.set_xlabel(r'$p_1$', fontsize=15)
ax.set_ylabel(r'$q_1$', fontsize=15)
ax.set_zlabel(r'$q_2$', fontsize=15)
plt.tick_params(labelsize=12)
ax.set_title("H=1.365416000", fontsize=15)
plt.show()
# Program 09c: Phase portrait and Poincare section of a nonautonomous ODE.
# See Figure 9.11(b): The Duffing equation.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
xmin=-2;xmax=2;ymin=-2;ymax=2;
k=0.3;omega=1.25;Gamma=0.5;
def dx_dt(x, t):
return [x[1], x[0] - k*x[1] - x[0]**3 + Gamma*np.cos(omega*t)]
# Phase portrait.
t=np.linspace(0,500,10000)
xs=odeint(dx_dt,[1,0],t)
plt.plot(xs[:,0],xs[:,1], "r-",lw=0.5)
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(xmin,xmax)
plt.ylim(ymin,ymax);
plt.show()
# The Poincare section.
x=[];y=[];
fig, ax = plt.subplots(figsize=(6,6))
t=np.linspace(0,4000*(2*np.pi)/omega,16000000)
xs=odeint(dx_dt,[1,0],t)
for i in range(4000):
x.extend([xs[4000*i,0]])
y.extend([xs[4000*i,1]])
ax.scatter(x,y, color='blue',s=0.1)
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 09d: Bifurcation diagram of the Duffing equation.
# See Figure 9.14. The system is history dependent.
# This can take about 20 seconds to complie.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
k = 0.3
omega = 1.25
alpha = 1
beta = -1
rs_up = []
rs_down = []
def duffing(x, t):
return [x[1],
-beta * x[0] - k*x[1] - alpha * x[0]**3 + gamma * np.cos(omega*t)]
# Take num_steps=4000 to get Figure 9.13.
num_steps = 4002
step = 0.0001
interval = num_steps * step
a, b = 1, 0
ns = np.linspace(0, num_steps, num_steps)
# Ramp the amplitude of vibration, gamma, up.
for n in ns:
gamma = step * n
t = np.linspace(0, (4*np.pi) / omega, 200)
xs = odeint(duffing, [a, b], t)
for i in range(2):
a = xs[100, 0]
b = xs[100, 1]
r = np.sqrt(a**2 + b**2)
rs_up.append([n, r])
rs_up = np.array(rs_up)
# Ramp the amplitude of vibration, gamma, down.
for n in ns:
gamma = interval - step * n
t = np.linspace(0, (4*np.pi) / omega, 200)
xs = odeint(duffing, [a, b], t)
for i in range(2):
a = xs[100, 0]
b = xs[100, 1]
r = np.sqrt(a**2 + b**2)
rs_down.append([num_steps - n, r])
rs_down = np.array(rs_down)
fig, ax = plt.subplots()
xtick_labels = np.linspace(0, interval, 5)
ax.set_xticks([x / interval * num_steps for x in xtick_labels])
ax.set_xticklabels(['{:.1f}'.format(xtick) for xtick in xtick_labels])
plt.plot(rs_up[:, 0], rs_up[:,1], 'r.', markersize=0.1)
plt.plot(rs_down[:, 0], rs_down[:,1], 'b.', markersize=0.1)
plt.xlabel(r'$\Gamma$', fontsize=15)
plt.ylabel('r', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 10a: Computing the Lienard Lyapunov quantities.
from sympy import symbols, solve
a2,a3,a4,a5,b2,b3,b4,b5=symbols('a2 a3 a4 a5 b2 b3 b4 b5')
V30,V21,V12,V03=symbols('V30 V21 V12 V03')
solve([3*V30-2*V12-b2,V12,V21+a2,2*V21-3*V03],[V30,V21,V12,V03])
V40,V31,V22,V13,V04,eta4=symbols('V40 V31 V22 V13 V04 eta4')
V4=solve([4*V40-2*V22-b3+2*a2**2,2*V22-4*V04,-eta4-V31-a3,V22,-2*eta4+3*V31-3*V13+2*a2*b2,-eta4+V13],\
[V40,V31,V22,V13,V04,eta4])
print(V4)
V50,V41,V32,V23,V14,V05=symbols('V50 V41 V32 V23 V14 V05')
V5=solve([5*V50-2*V32-b4+10*a2**2*b2/3,3*V32-4*V14,V14,-V41-a4+2*a2**3,4*V41-3*V23+2*a2*b3,2*V23-5*V05],\
[V50,V41,V32,V23,V14,V05])
print(V5)
V60,V51,V42,V33,V24,V15,V06,eta6=symbols('V60 V51 V42 V33 V24 V15 V06 eta6')
V6=solve([6*V60-2*V42-b5+6*a2*a4+4*a2**2*b2**2/3-8*a2**4,\
4*V42-4*V24-16*a2**4/3-4*a2**2*b3/3+8*a2*a4/3,\
V24-6*V06,\
V42+V24,\
-eta6-V51-a5+8*a2**3*b2/3,\
-3*eta6+5*V51-3*V33+2*a2*b4-8*a2**3*b2-2*a2*b2*b3+4*a4*b2,\
-3*eta6+3*V33-5*V15-16*a2**3*b2/3-4*a2*b2*b3/3+8*a4*b2/3,\
-eta6+V15],\
[V60,V51,V42,V33,V24,V15,V06,eta6])
print(V6)
{V40: -a2**2/2 + b3/4, V22: 0, V04: 0, V31: -a2*b2/4 - 5*a3/8, V13: a2*b2/4 - 3*a3/8, eta4: a2*b2/4 - 3*a3/8}
{V50: -2*a2**2*b2/3 + b4/5, V32: 0, V14: 0, V41: 2*a2**3 - a4, V23: 8*a2**3/3 + 2*a2*b3/3 - 4*a4/3, V05: 16*a2**3/15 + 4*a2*b3/15 - 8*a4/15}
{V60: -2*V06 + 4*a2**4/3 - 2*a2**2*b2**2/9 - a2*a4 + b5/6, V42: -6*V06, V24: 6*V06, V51: 8*a2**3*b2/3 + 5*a2*b2*b3/24 - a2*b4/8 - 5*a4*b2/12 - 11*a5/16, V33: 16*a2**3*b2/9 - a2*b2*b3/9 + a2*b4/3 + 2*a4*b2/9 - 5*a5/6, V15: -5*a2*b2*b3/24 + a2*b4/8 + 5*a4*b2/12 - 5*a5/16, eta6: -5*a2*b2*b3/24 + a2*b4/8 + 5*a4*b2/12 - 5*a5/16}
# Program 10b: Polynomial Reduce. See Example 4.
from sympy import reduced
from sympy.abc import x,y,z
f=x**4+y**4+z**4
p=reduced(f,[x**2+y,z**2*y-1,y-z**2])
print(p)
q=reduced(f,[y-z**2,z**2*y-1,x**2+y])
print(q)
([x**2 - y, y**2 + 2, y**3 + 2*y], z**4 + 2) ([-x**2 + y**3 + y**2*z**2 + y*z**4 + z**6 + z**2, 0, x**2 - z**2], z**8 + 2*z**4)
# Program 10c: The S-Polynomial. See Example 5.
from sympy import expand, LM, LT, lcm
from sympy.abc import x,y,z
def s_polynomial(f, g):
return expand(lcm(LM(f), LM(g))*(1/LT(f)*f - 1/LT(g)*g))
F=[f, g]=[x-13*y**2-12*z**3, x**2-x*y+92*z]
S=s_polynomial(f,g)
print(S)
-13*x*y**2 + x*y - 12*x*z**3 - 92*z
# Program 10d: Computing Groebner bases. See Example 6.
from sympy import groebner
from sympy.abc import x,y
G=groebner([x+y**2-x**3, 4*x**3-12*x*y**2+x**4+2*x**2*y**2+y**4],order='lex')
print(G)
GroebnerBasis([5970075*x + 160356*y**10 + 14472880*y**8 - 162599547*y**6 + 163845838*y**4 + 5970075*y**2, y**12 + 90*y**10 - 1037*y**8 + 1278*y**6 - 195*y**4], x, y, domain='ZZ', order='lex')
# Program 10e: Computing Groebner bases. See Example 7.
# Reducing the first five Lyapunov quantities of a Lienard system.
from sympy import groebner, symbols
a1,a2,a3,a4,b2,b3=symbols('a1 a2 a3 a4 b2 b3')
G=groebner([-a1,2*a2*b2-3*a3,5*b2*(2*a4-b3*a2),\
-5*b2*(92*b2**2*a4-99*b3**2*a2+1520*a2**2*a4-760*a2**3*b3-46*b2**2*b3*a2+198*b3*a4),\
-b2*(14546*b2**4*a4+105639*a2**3*b3**2+96664*a2**3*b2**2*b3-193328*a2**2*b2**2*a4-\
891034*a2**4*a4+445517*a2**5*b3+211632*a2*a4**2-317094*a2**2*b3*a4-44190*b2**2*b3*a4+\
22095*b2**2*b3**2*a2-7273*b2**4*b3*a2+5319*b3**3*a2-10638*b3**2*a4)],order='lex')
print(G)
GroebnerBasis([a1, 2*a2*b2 - 3*a3, 3*a3*b3 - 4*a4*b2], a1, a2, a3, a4, b2, b3, domain='ZZ', order='lex')
# Program 10f: First homoclinic limit cycle bifurcation animation. See Figure 10.2.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
fig=plt.figure()
plt.axis([-1.5, 1.5, -1.5, 1.5])
myimages=[]
def Homoclinic1(x, t):
return [x[1]+10*x[0]*(0.1-x[1]**2), -x[0]+C]
time = np.arange(0, 200, 0.01)
x0=[1,0]
for C in np.arange(-0.2, 0.2, 0.01):
xs = odeint(Homoclinic1, x0, time)
imgplot = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot)
my_anim = animation.ArtistAnimation(fig,myimages,interval=100,blit=False,repeat_delay=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())
# Program 10g: Second homoclinic limit cycle bifurcation. See Figure 10.3.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
fig=plt.figure()
plt.axis([-2, 0.5, -1, 1])
myimages=[]
def Homoclinic2(x, t):
return [x[1], x[0]+x[0]**2-x[0]*x[1]+L*x[1]]
time = np.arange(0, 50, 0.005)
x0=[-0.1,0.1]
for L in np.arange(-2, -0.5, 0.01):
xs = odeint(Homoclinic2, x0, time)
imgplot2 = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot2)
my_anim = animation.ArtistAnimation(fig,myimages,interval=100,blit=False,repeat_delay=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())
# Program 11a: Animation of a limit cycle for a Lienard system.
# See Figure 11.12.
from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np
from scipy.integrate import odeint
%matplotlib notebook
fig=plt.figure()
xmin, xmax, ymin, ymax = -4, 4, -15, 15
ax=plt.axes(xlim=(xmin,xmax),ylim=(ymin,ymax))
myimages=[]
def Lienard(x, t):
return [mu*x[1] - mu*(- 4*x[0] + x[0]**3), - x[0]/mu]
time = np.arange(0.1, 20, 0.1)
x0=[2,0]
for mu in np.arange(0.1, 10, 0.01):
xs = odeint(Lienard, x0, time)
imgplot = plt.plot(xs[:,0], xs[:,1], "r-")
myimages.append(imgplot)
anim = animation.ArtistAnimation(fig, myimages, interval = 100,\
blit = False, repeat_delay = 100)
plt.show()
# Program 11b: Small-amplitude limit cycles.
# A cubic Lienard system. See Figure 10.1 and Table 11.1.
# Limit cycles are shown as blue trajectories.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
a1, a2, a3, b2, b3 = 0.01, 1, 1/3, 1, 2
xmin, xmax, ymin, ymax = -1, 1, -0.6, 1.4
# The Lienard system
def Lienard(x, t):
# Here x[0] = x and x[1] = y
return np.array([ x[1] - a1*x[0] - a2*x[0]**2 - a3*x[0]**3, \
-x[0] - a1*x[1] - b2*x[0]**2 - b3*x[0]**3 ])
t = np.linspace(0, 200, 1000)
# Trajectories in forward time move away from inner limit cycle.
xs=odeint(Lienard,[0.25,0],np.linspace(0,20,5000))
plt.plot(xs[:,0],xs[:,1], "r-")
# Unstable limit cycle.
# Trajectories in backwards time move towards the limit cycle.
xs=odeint(Lienard,[0.295,0],np.linspace(0,-50,5000))
plt.plot(xs[:,0],xs[:,1], 'b-', linewidth=2)
# Trajectories in forward time move away from inner limit cycle.
xs=odeint(Lienard,[0.32,0],np.linspace(0,20,5000))
plt.plot(xs[:,0],xs[:,1], 'r-')
# Trajectories in forward time move towards the outer limit cycle.
xs=odeint(Lienard,[0.44,0],np.linspace(0,22,5000))
plt.plot(xs[:,0],xs[:,1], 'r-')
# Stable limit cycle.
xs=odeint(Lienard,[0.519,0],np.linspace(0,50,5000))
plt.plot(xs[:,0],xs[:,1], 'b-', linewidth=2)
# Trajectories in forward time move towards the outer limit cycle.
xs=odeint(Lienard,[0.6,0],np.linspace(0,22,5000))
plt.plot(xs[:,0],xs[:,1], 'r-')
# Label the axes and set fontsizes.
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.xlim(xmin,xmax)
plt.ylim(ymin,ymax);
plt.show()
# Program 12a: The method of steps.
# See Figure 12.1.
from sympy import integrate,symbols
xi,t,i=symbols('xi t i')
def phi(i,t):
if i==0:
return 1 # Initial history x(t)=1 on [-1,0].
else:
return phi(i-1,i-1)-integrate(phi(i-1,xi-1),(xi,i-1,t))
x=[]
tmax=10;
for j in range(tmax+1):
p=phi(j,t)
x.append(p)
print('x(t)=',x)
x(t)= [1, 1 - t, t**2/2 - 2*t + 3/2, -t**3/6 + 3*t**2/2 - 4*t + 17/6, t**4/24 - 2*t**3/3 + 15*t**2/4 - 17*t/2 + 149/24, -t**5/120 + 5*t**4/24 - 2*t**3 + 109*t**2/12 - 115*t/6 + 1769/120, t**6/720 - t**5/20 + 35*t**4/48 - 197*t**3/36 + 1061*t**2/48 - 1085*t/24 + 26239/720, -t**7/5040 + 7*t**6/720 - t**5/5 + 107*t**4/48 - 521*t**3/36 + 13081*t**2/240 - 13201*t/120 + 463609/5040, t**8/40320 - t**7/630 + 7*t**6/160 - 487*t**5/720 + 3685*t**4/576 - 27227*t**3/720 + 39227*t**2/288 - 39371*t/144 + 3157891/13440, -t**9/362880 + t**8/4480 - t**7/126 + 701*t**6/4320 - 1511*t**5/720 + 51193*t**4/2880 - 212753*t**3/2160 + 1156699*t**2/3360 - 1158379*t/1680 + 43896157/72576, t**10/3628800 - t**9/36288 + 11*t**8/8960 - 323*t**7/10080 + 1873*t**6/3456 - 89269*t**5/14400 + 279533*t**4/5760 - 7761511*t**3/30240 + 23602499*t**2/26880 - 23615939*t/13440 + 5681592251/3628800]
# Program 12b: Solution of a DDE using the method of steps.
# See Figure 12.1. The plot is a piecewise function.
# The lambda t: functions are computed in Programs 12a.
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-1, 10, 1000)
plt.plot(t, np.piecewise(t, [t<=0,t>0,t>1,t>2,t>3,t>4,t>5,t>6,t>7,t>8,t>9],
[lambda t: 1,
lambda t: 1-t,
lambda t: t**2/2-2*t+3/2,
lambda t: -t**3/6+3*t**2/2-4*t+17/6,
lambda t: t**4/24-2*t**3/3+15*t**2/4-17*t/2+149/24,
lambda t: -t**5/120 + 5*t**4/24 - 2*t**3 + 109*t**2/12
- 115*t/6 + 1769/120,
lambda t: t**6/720 - t**5/20 + 35*t**4/48 - 197*t**3/36
+ 1061*t**2/48 - 1085*t/24 + 26239/720,
lambda t: -t**7/5040 + 7*t**6/720 - t**5/5 + 107*t**4/48 -
521*t**3/36 + 13081*t**2/240 - 13201*t/120 + 463609/5040,
lambda t: t**8/40320 - t**7/630 + 7*t**6/160 - 487*t**5/720 +
3685*t**4/576 - 27227*t**3/720 + 39227*t**2/288 - 39371*t/144
+ 3157891/13440,
lambda t: -t**9/362880 + t**8/4480 - t**7/126 + 701*t**6/4320 -
1511*t**5/720 + 51193*t**4/2880 - 212753*t**3/2160 + 1156699*t**2/3360
- 1158379*t/1680 + 43896157/72576,
lambda t: t**10/3628800 - t**9/36288 + 11*t**8/8960 - 323*t**7/10080 +
1873*t**6/3456 - 89269*t**5/14400 + 279533*t**4/5760 - 7761511*t**3/30240 +
23602499*t**2/26880 - 23615939*t/13440 + 5681592251/3628800
]))
plt.xlabel("t",fontsize=25)
plt.ylabel("x(t)",fontsize=25)
plt.tick_params(labelsize=25)
plt.show()
# Program 12c: The Mackey-Glass DDE.
# See Figure 12.5(a).
# pydelay must be on your computer.
import pylab as pl
from pydelay import dde23
# define the equations
eqns = {
'x' : '2 * x(t-tau) / (1.0 + pow(x(t-tau),p)) - x'
}
#define the parameters
params = {
'tau': 2,
'p' : 10
}
# Initialise the solver
dde = dde23(eqns=eqns, params=params)
# set the simulation parameters
# (solve from t=0 to t=1000 and limit the maximum step size to 1.0)
dde.set_sim_params(tfinal=1000, dtmax=1.0)
# set the history of to the constant function 0.5 (using a python lambda function)
histfunc = {
'x': lambda t: 0.5
}
dde.hist_from_funcs(histfunc, 51)
# run the simulator
dde.run()
# Make a plot of x(t) vs x(t-tau):
# Sample the solution twice with a stepsize of dt=0.1:
# once in the interval [515, 1000]
sol1 = dde.sample(515, 1000, 0.1)
x1 = sol1['x']
# and once between [500, 1000-15]
sol2 = dde.sample(500, 1000-15, 0.1)
x2 = sol2['x']
pl.plot(x1, x2)
pl.xlabel('$x(t)$')
pl.ylabel('$x(t - 15)$')
pl.show()

# Program 12d: The Lang-Kobayashi DDEs.
# See Figure 12.10.
# pydelay must be on your computer.
import numpy as np
import pylab as pl
from pydelay import dde23
tfinal = 10000
tau = 1000
#the laser equations
eqns = {
'E:c': '0.5*(1.0+ii*a)*E*n + K*E(t-tau)',
'n' : '(p - n - (1.0 +n) * pow(abs(E),2))/T'
}
params = {
'a' : 4.0,
'p' : 1.0,
'T' : 200.0,
'K' : 0.1,
'tau': tau,
'nu' : 10**-5,
'n0' : 10.0
}
noise = { 'E': 'sqrt(0.5*nu*(n+n0)) * (gwn() + ii*gwn())' }
dde = dde23(eqns=eqns, params=params, noise=noise)
dde.set_sim_params(tfinal=tfinal)
# use a dictionary to set the history
thist = np.linspace(0, tau, tfinal)
Ehist = np.zeros(len(thist))+1.0
nhist = np.zeros(len(thist))-0.2
dic = {'t' : thist, 'E': Ehist, 'n': nhist}
# 'useend' is True by default in hist_from_dict and thus the
# time array is shifted correctly
dde.hist_from_arrays(dic)
dde.run()
t = dde.sol['t']
E = dde.sol['E']
n = dde.sol['n']
spl = dde.sample(-tau, tfinal, 0.1)
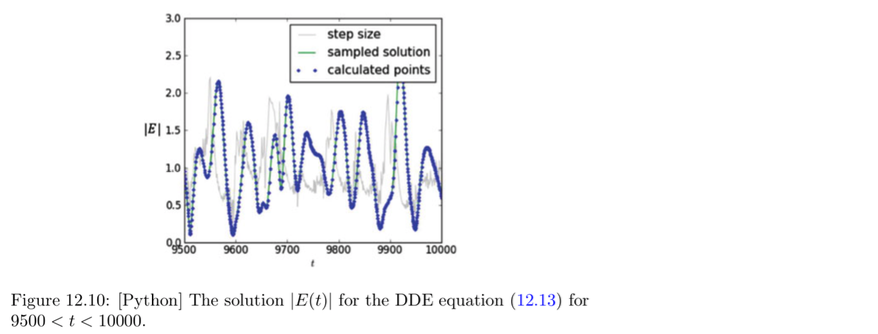
pl.plot(t[:-1], t[1:] - t[:-1], '0.8', label='step size')
pl.plot(spl['t'], abs(spl['E']), 'g', label='sampled solution')
pl.plot(t, abs(E), '.', label='calculated points')
pl.legend()
pl.xlabel('$t$')
pl.ylabel('$|E|$')
pl.xlim((0.95*tfinal, tfinal))
pl.ylim((0,3))
pl.show()
# Program 13a: Recurrence relations, interest in a bank account.
from sympy import Function, rsolve
from sympy.abc import n
x=Function('x');
f=x(n+1)-(1+3/100)*x(n);
sol=rsolve(f,x(n),{x(0):10000});
print('x_n=',sol)
x_5=round(sol.subs(n,5),2)
print('x(5)=£',x_5)
x_n= 10000*1.03**n x(5)=£ 11592.74
# Program 13b: A second order recurrence relation.
# See Example 2.
from sympy import Function, rsolve
from sympy.abc import n
x = Function('x');
f = x(n+2) - x(n+1) - 6*x(n);
sol=rsolve(f, x(n), {x(0):1,x(1):2});
print('x_n=', sol)
x_n= (-2)**n/5 + 4*3**n/5
# Program 13c: The Leslie matrix. See Example 4.
# Compute the population distribution after 50 years.
# Determine the eigenvalues and eigenvectors of a Leslie matrix.
import numpy as np
import numpy.linalg as LA
L=np.array([[0,3,1],[0.3,0,0],[0,0.5,0]])
X0=np.array([[1000],[2000],[3000]])
X_50=np.dot(LA.matrix_power(L,50),X0)
X_50=X_50.round()
print('X(50)=',X_50)
dL,VL=LA.eig(L)
print('Eigenvalues=',dL)
print('Eigenvectors=',VL)
X(50)= [[15696.] [ 4604.] [ 2249.]] Eigenvalues= [ 1.02304502 -0.85068938 -0.17235564] Eigenvectors= [[ 0.95064458 -0.92555739 0.18403341] [ 0.27876913 0.32640259 -0.32032617] [ 0.1362448 -0.19184593 0.9292593 ]]
# Program 13d: The Leslie matrix population plot. See Example 4.
# Plot the population distribution for 0<t<50 years.
# In this case, one age class is one year.
import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
t_span = 51
L=np.array([[0,3,1],[0.3,0,0],[0,0.5,0]])
X=[0]*t_span;X1=[0]*t_span;X2=[0]*t_span;X3=[0]*t_span;
X[0]=np.array([[1000],[2000],[3000]])
for i in range(t_span):
X[i] =np.array(np.dot(LA.matrix_power(L,i),X[0])).tolist()
X1[i] = X[i][0]
X2[i] = X[i][1]
X3[i] = X[i][2]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X1,color='r',label='Age Class 1')
ax.plot(X2,color='b',label='Age Class 2')
ax.plot(X3,color='k',label='Age Class 3')
plt.xlabel("Age classes",fontsize=15)
plt.ylabel("Populations",fontsize=15)
plt.tick_params(labelsize=15)
legend = plt.legend(loc='upper center',shadow=True)
plt.show()
# Program 14a: Graphical iteration of the tent map.
# See Figure 14.7(a).
from sympy import Rational
import numpy as np
import matplotlib.pyplot as plt
x=Rational(1,5) # Initial value
inputs = np.array([])
outputs = np.array([])
inputs = np.append(inputs,x)
outputs = np.append(outputs,0)
print(x)
for i in range(2,10):
inputs = np.append(inputs,x)
inputs = np.append(inputs,x)
outputs = np.append(outputs,x)
if x < Rational(1,2):
x = 2 * x
elif x > Rational(1,2):
x = 2 - 2 * x
outputs = np.append(outputs,x)
print(x)
plt.plot(inputs,outputs,lw=2)
# Plot the tent function and line y=x.
X1 = np.linspace(0,0.5,100,endpoint=True)
X2=np.linspace(0.5,1,100,endpoint=True)
X=np.linspace(0,1,200,endpoint=True)
plt.plot(X1,2*X1,'k-')
plt.plot(X2,2*(1-X2),'k-')
plt.plot(X,X,'r-')
plt.xlabel("x",fontsize=15)
plt.ylabel("T(x)",fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
1/5 2/5 4/5 2/5 4/5 2/5 4/5 2/5 4/5
# Program 14b: Bifurcation diagram of the logistic map.
# See Figures 14.15 and 14.16.
import numpy as np
import matplotlib.pyplot as plt
def f(x, r):
return r * x * (1-x)
if __name__ == "__main__":
ys = []
rs = np.linspace(0, 4, 2000)
#rs = np.linspace(3.5, 4, 2000) # For Figure 14.16.
for r in rs:
x = 0.1
for i in range(500):
x = f(x, r)
for i in range(50):
x = f(x, r)
ys.append([r, x])
ys = np.array(ys)
plt.plot(ys[:,0],ys[:,1],'r.',markersize=0.05)
plt.xlabel("$\mu$",fontsize=15)
plt.ylabel("x",fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 14c: Lyapunov exponents of the logistic map.
# See Figure 14.17.
import numpy as np
import matplotlib.pyplot as plt
Numpoints=16000;
result = []
lambdas = []
maps = []
xmin = 3
xmax = 4
mult=(xmax-xmin)*Numpoints
muvalues = np.arange(xmin, xmax, 20/Numpoints)
for r in muvalues:
x = 0.1
result = []
for t in range(100):
x = r * x * (1 - x)
result.append(np.log(abs(r - 2*r*x)))
lambdas.append(np.mean(result))
# Ignore first 100 iterates.
for t in range(20):
x = r * x * (1 - x)
maps.append(x)
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(1,1,1)
xticks = np.linspace(xmin, xmax, mult)
zero = [0]*mult
ax1.plot(xticks,zero,'k-',linewidth=3)
ax1.plot(xticks, maps,'r.',alpha = 0.3,label='Logistic map')
ax1.set_xlabel('r')
ax1.plot(muvalues,lambdas,'b-',linewidth= 1,label='Lyapunov exponent')
ax1.grid('on')
ax1.set_ylim(-1, 1)
ax1.set_xlabel('$\mu$',fontsize=15)
ax1.legend(loc='best')
ax1.set_title('Logistic map versus Lyapunov exponent',fontsize=15)
plt.show()
# Program 14d: Iteration of the Henon Map.
# See Figure 14.23: Chaotic attractor.
import matplotlib.pyplot as plt
# Parameters
a=1.2;b=0.4; # Set a=1 to get Figure 14.23(a).
Num_iterations=10000;
def Henon(X):
x, y = X
xn = 1 - a*x*x + y
yn = b*x
return xn,yn
# Ignore the first 100 iterates.
X0=[(1-b)/2, (1-b)/2]
X,Y=[],[]
for i in range(100):
xn,yn=Henon(X0)
X,Y = X + [xn], Y + [yn]
X0=[xn,yn]
X,Y=[],[]
for i in range(Num_iterations):
xn,yn=Henon(X0)
X, Y = X + [xn], Y + [yn]
X0=[xn,yn]
fig, ax = plt.subplots(figsize=(6,6))
ax.scatter(X,Y,color='blue',s=0.1)
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 14e: Lyapunov exponents of the Henon map.
# See Exercise 8(c).
import numpy as np
a=1.2;b=0.4;x=0;y=0;
vec1=[1,0];vec2=[0,1];
for i in range(490):
xn = 1 - a*x*x + y
yn = b*x
x=xn;y=yn;
J=np.array([[-2*a*x, 1],[b, 0]])
vec1=J.dot(vec1)
vec2=J.dot(vec2)
dotprod1=np.dot(vec1,vec1)
dotprod2=np.dot(vec1,vec2)
vec2=vec2-np.multiply((dotprod2/dotprod1),vec1)
lengthv1=np.sqrt(dotprod1)
area=np.multiply(vec1[0],vec2[1])-np.multiply(vec1[1],vec2[0])
h1=np.log(lengthv1)/i
h2=np.log(area)/i-h1
print('h_1=',h1)
print('h_2=',h2)
h_1= 0.3391568093091681 h_2= -1.2565387259040743
<ipython-input-49-5562481e6be6>:20: RuntimeWarning: divide by zero encountered in double_scalars h1=np.log(lengthv1)/i <ipython-input-49-5562481e6be6>:21: RuntimeWarning: invalid value encountered in log h2=np.log(area)/i-h1
# Programs 14f: Graphical iteration of the logistic map.
# See Figure 14.14.
import numpy as np
import matplotlib.pyplot as plt
x = 0.2 # Initial value
inputs = np.array([x])
outputs = np.array([0])
for i in range(2, 100):
inputs = np.append(inputs, x)
inputs = np.append(inputs, x)
outputs = np.append(outputs, x)
x = 4 * x * (1 - x)
outputs = np.append(outputs, x)
plt.plot(inputs, outputs, 'b-', lw=0.2)
# Plot the logistic map function and line y=x.
X = np.linspace(0, 1, 200, endpoint=True)
plt.plot(X, 4 * X * (1 - X), 'k-')
plt.plot(X, X, 'r-')
plt.xlabel('x', fontsize=15)
plt.ylabel('$f_{\mu}(x)$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 15a: Plot points for the Julia set.
# See Figure 15.1.
from matplotlib import pyplot as plt
import random
from sympy import sqrt,re,im,I
# Parameters
a =0;b=1.1; # To plot J(a,b).
k=15
Num_iterations=2**k
def Julia(X):
x, y = X
x1=x;y1=y;
u = sqrt((x1-a)**2+(y1-b)**2)/2
v=(x-a)/2
u1=sqrt(u+v)
v1=sqrt(u-v)
xn=u1;yn=v1;
if y1<b:
yn=-yn
if random.random() < 0.5:
xn=-u1
yn=-yn
return xn, yn
x1=(re(0.5+sqrt(0.25-(a+b*I)))).expand(complex=True)
y1=(im(0.5+sqrt(0.25-(a+b*I)))).expand(complex=True)
isunstable=2*abs(x1+y1*I)
print(isunstable)
X0 = [x1, y1]
X, Y = [], []
for i in range(Num_iterations):
xn, yn = Julia(X0)
X, Y = X + [xn], Y + [yn]
X0 = [xn, yn]
fig, ax = plt.subplots(figsize=(6,6))
ax.scatter(X, Y, color='blue', s=0.15)
ax.axis('off')
plt.show()
2.97195366175600
# Program 15b: Colormap of a Julia set.
# See Figure 15.2.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm # Use a colormap.
# Set image dimensions.
Im_w, Im_h = 500, 500
c = complex(-0.1,0.65) # To plot J(a,b).
Max_abs_z = 10
Max_iter = 1000
xmin, xmax = -2, 2
xrange = xmax - xmin
ymin, ymax = -2, 2
yrange = ymax - ymin
Julia = np.zeros((Im_w, Im_h))
for Re_z in range(Im_w):
for Im_y in range(Im_h):
nit = 0
# Map pixel position to a point in the plane
z = complex(Re_z / Im_w * xrange+ xmin,
Im_y / Im_h * yrange + ymin)
# Do the iterations
while abs(z) <= Max_abs_z and nit < Max_iter:
z = z**2 + c
nit += 1
ratio = nit / Max_iter
Julia[-Im_y,Re_z] = ratio # Set axes to Re(z) and Im(z).
fig, ax = plt.subplots(figsize=(6,6))
ax.axis('off')
ax.imshow(Julia, interpolation='nearest', cmap=cm.hot)
plt.show()
# Program 15c: The Mandelbrot set.
# See Figure 15.3.
import matplotlib.pyplot as plt
import numpy as np
xmin, xmax, ymin, ymax = -2.5, 1, -1.5, 1.5
xrange = xmax - xmin
yrange = ymax - ymin
def get_iter(c:complex, thresh:int =4, max_steps:int =25) -> int:
# Z_(n+1) = (Z_(n))^2 + c
# Z_(0) = c
z, i = c, 1
while i<max_steps and (z*z.conjugate()).real<thresh:
z = z * z + c
i+=1
return i
def plotter(n, thresh, max_steps = 25):
mapper = lambda x, y: (4*(x-n//2)/n, 4*(y-n//2)/n)
img = np.full((n,n), 255)
x_lower = 0
x_upper = 5*n//8
y_lower = 2*n//10
y_upper = 8*n//10
for x in range(x_lower, x_upper):
for y in range(y_lower, y_upper):
it = get_iter(complex(*mapper(x,y)), thresh=thresh, max_steps=max_steps)
img[y][x] = 255 - it
return img[y_lower:y_upper, x_lower:x_upper]
n=1000
img = plotter(n, thresh=4, max_steps=50)
fig, ax = plt.subplots(figsize=(7,7))
plt.imshow(img, cmap = cm.seismic)
plt.axis("off")
plt.show()
# Program 15d: The Newton fractal for f(z)=z**3-1.
# Newton-Rapshon method.
# See Figure 15.7 (alternative form to book).
from PIL import Image
import numpy as np
epsilon, scale, niters = 0.0001, 600, 40
xmin, xmax = -1.5, 1.5
ymin, ymax = -1.5, 1.5
# Create blank image.
img=Image.new("RGB", (scale, scale), (0, 0, 0))
# Roots of z**3-1 = 0 (Euler's formula).
roots = [np.cos((2*n)*np.pi/3)+1j*np.sin((2*n)*np.pi/3) for n in range(3)]
colors = [(1, 0, 0), (0, 1, 0), (0, 0, 1)] # RGB.
for re in range(scale):
zx=re*(xmax-xmin)/(scale-1)+xmin
for im in range(scale):
zy=im*(ymax-ymin)/(scale-1)+ymin
z=complex(zx, zy)
for i in range(niters):
try:
z -= (z**3-1)/(3*z**2)
except ZeroDivisionError:
# Divide by zero exception.
continue
if(abs(z**3-1) < epsilon):
break
# Shade colors.
color_shade = int((niters-i)*255.0/niters)
# RGB roots.
err = [ abs(z-root) for root in roots ]
distances = zip(err, range(len(colors)))
# Select color.
color = [i*color_shade for i in colors[min(distances)[1]]]
img.putpixel((re, im), tuple(color))
img.save('Newton_Fractal.png','PNG')
img.show()

# Program 16a: Intersection of implicit curves.
# See Figure 16.10(b): To find fixed points of period one.
import numpy as np
import matplotlib.pyplot as plt
A, B = 2.2, 0.15
x, y = np.mgrid[0:4:100j, -4:4:100j]
z1 = A + B*x*np.cos(x**2 + y**2) - B*y*np.sin(x**2 + y**2) - x
z2 = B*x*np.sin(x**2 + y**2) + B*y*np.cos(x**2 + y**2) - y
fig, ax = plt.subplots()
plt.contour(x, y, z1, levels=[0])
plt.contour(x, y, z2, levels=[0], colors='r')
ax.set_xlabel('x(t)', fontsize=15)
ax.set_ylabel('y(t)', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 16b: Iteration of the Ikeda map.
# See Figure 16.11(b): Chaotic attractor.
from matplotlib import pyplot as plt
import numpy as np
# Parameters
A, B = 10, 0.15
def ikeda(X):
x, y = X
xn = A + B*x*np.cos(x**2 + y**2) - B*y*np.sin(x**2 + y**2)
yn = B*x*np.sin(x**2 + y**2) + B*y*np.cos(x**2 + y**2)
return (xn, yn)
X0 = [A, 0]
X, Y = [], []
for i in range(10000):
xn, yn = ikeda(X0)
X, Y = X + [xn], Y + [yn]
X0 = [xn, yn]
fig, ax = plt.subplots(figsize=(6,6))
ax.scatter(X, Y, color='blue', s=0.1)
plt.xlabel('$Re(E_n)$', fontsize=15)
plt.ylabel('$Im(E_n)$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 16c: Bifurcation diagram of the Ikeda map.
# See Figure 16.16(d). Instabilities encroach on hysteresis.
from matplotlib import pyplot as plt
import numpy as np
# Parameters
C = 0.345913
kappa = 0.0225
Pmax = 120
phi = np.pi
half_N = 4999
N = 2*half_N + 1
N1 = 1 + half_N
esqr_up, esqr_down = [], []
E1 = E2 = 0
ns_up = np.arange(half_N)
ns_down = np.arange(N1, N)
# Ramp the power up
for n in ns_up:
E2 = E1 * np.exp(1j*((abs(C*E1))**2 - phi))
E1 = 1j * np.sqrt(1 - kappa) * np.sqrt(n * Pmax / N1) + \
np.sqrt(kappa) * E2
esqr1 = abs(E1)**2
esqr_up.append([n, esqr1])
esqr_up = np.array(esqr_up)
# Ramp the power down
for n in ns_down:
E2 = E1 * np.exp(1j * ((abs(C*E1))**2 - phi))
E1 = 1j * np.sqrt(1 - kappa) * np.sqrt(2 * Pmax - n * Pmax / N1) \
+ np.sqrt(kappa) * E2
esqr1 = abs(E1)**2
esqr_down.append([N-n, esqr1])
esqr_down=np.array(esqr_down)
fig, ax = plt.subplots()
xtick_labels = np.linspace(0, Pmax, 6)
ax.set_xticks([x / Pmax * N1 for x in xtick_labels])
ax.set_xticklabels(['{:.1f}'.format(xtick) for xtick in xtick_labels])
plt.plot(esqr_up[:, 0], esqr_up[:, 1], 'r.', markersize=0.1)
plt.plot(esqr_down[:, 0], esqr_down[:, 1], 'b.', markersize=0.1)
plt.xlabel('Input', fontsize=15)
plt.ylabel('Output', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 16d: Animation of the Ikeda Chaotic Attractor.
from matplotlib import pyplot as plt
from matplotlib.animation import ArtistAnimation
import numpy as np
fig=plt.figure()
plt.title('Animation Ikeda Chaotic Attractor')
plt.axis([0, 14, -2, 2])
B = 0.15
def ikeda(X):
x, y = X
xn = A + B*x*np.cos(x**2 + y**2) - B*y*np.sin(x**2 + y**2)
yn = B*x*np.sin(x**2 + y**2) + B*y*np.cos(x**2 + y**2)
return (xn, yn)
myimages = []
for A in np.arange(2, 10, 0.1):
X0 = [A, 0]
X, Y = [], []
for i in range(5000):
xn, yn = ikeda(X0)
X, Y = X + [xn], Y + [yn]
X0 = [xn, yn]
myimages.append(plt.plot(X, Y, 'b.', markersize=0.2))
anim = ArtistAnimation(fig, myimages, blit=False, interval=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())

# Programs 17a: Plotting the Koch curve.
# See Figure 17.2.
import numpy as np
import matplotlib.pyplot as plt
from math import floor
k=6
n_lines = 4**k
h = 3**(-k);
x = [0]*(n_lines+1)
y = [0]*(n_lines+1)
x[0], y[0] = 0, 0
segment=[0] * n_lines;
# The angles of the four segments.
angle=[0, np.pi/3, -np.pi/3, 0]
for i in range(n_lines):
m=i
ang=0
for j in range(k):
segment[j] = np.mod(m, 4)
m = floor(m / 4)
ang = ang + angle[segment[j]]
x[i+1] = x[i] + h*np.cos(ang)
y[i+1] = y[i] + h*np.sin(ang)
plt.axis('equal')
plt.plot(x,y)
plt.show()
# Program 17b: The chaos game and Sierpinski triangle.
# See Figure 17.6.
import matplotlib.pyplot as plt
from random import random, randint
import numpy as np
def midpoint(P, Q):
return (0.5*(P[0] + Q[0]), 0.5*(P[1] + Q[1]))
# The three vertices.
vertices = [(0, 0), (2, 2*np.sqrt(3)), (4, 0)]
iterates = 50000
x, y = [0]*iterates, [0]*iterates
x[0], y[0] = random(), random()
for i in range(1, iterates):
k = randint(0, 2)
x[i], y[i] = midpoint(vertices[k], (x[i-1], y[i-1]))
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(x, y, color='r', s=0.1)
ax.axis('off')
plt.show()
# Program 17c: Barnsley's fern.
# See Figure 17.7.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# The transformation T
f1 = lambda x, y: (0.0, 0.2*y)
f2 = lambda x, y: (0.85*x + 0.05*y, -0.04*x + 0.85*y + 1.6)
f3 = lambda x, y: (0.2*x - 0.26*y, 0.23*x + 0.22*y + 1.6)
f4 = lambda x, y: (-0.15*x + 0.28*y, 0.26*x + 0.24*y + 0.44)
fs = [f1, f2, f3, f4]
num_points = 60000
width = height = 300
fern = np.zeros((width, height))
x, y = 0, 0
for i in range(num_points):
# Choose a random transformation
f = np.random.choice(fs, p=[0.01, 0.85, 0.07, 0.07])
x, y = f(x,y)
# Map (x,y) to pixel coordinates
# Center the image
cx, cy = int(width / 2 + x * width / 10), int(y * height / 10)
fern[cy, cx] = 1
fig, ax=plt.subplots(figsize=(6,6))
plt.imshow(fern[::-1,:], cmap=cm.Greens)
ax.axis('off')
plt.show()
# Program 17d: Plot tau curve, D_q curve and f(alpha) curve.
# See Figure 17.16: Multifractal spectra.
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
plt.subplots_adjust(hspace=1)
plt.figure(1)
# The tau curve
x = np.linspace(-20, 20, 1000)
y = (np.log((1/9)**x + (8/9)**x) / np.log(3))
plt.subplot(3, 1, 1)
plt.plot(x, y)
plt.xlabel('$q$', fontsize=15)
plt.ylabel(r'$\tau(q)$', fontsize=15)
plt.tick_params(labelsize=15)
# The D_q curve
x1 = np.linspace(-20, 0.99, 100)
x2 = np.linspace(0.99, 20, 100)
Dq1 = (np.log((1/9)**x1 + (8/9)**x1) / (np.log(3) * (1 - x1)))
Dq2 = (np.log((1/9)**x2 + (8/9)**x2) / (np.log(3) * (1 - x2)))
plt.subplot(3, 1, 2)
plt.plot(x1, Dq1, x2, Dq2)
plt.xlabel('q', fontsize=15)
plt.ylabel('$D_q$', fontsize=15)
plt.tick_params(labelsize=15)
# The f(alpha) curve
p1, p2 = 1/9, 8/9
k = 500
s = np.arange(500)
x = (s*np.log(p1) + (k-s) * np.log(p2)) / (k*np.log(1/3))
f = -(np.log(comb(k, s))) / (k*np.log(1/3))
plt.subplot(3, 1, 3)
plt.plot(x, f)
plt.xlabel(r'$\alpha$', fontsize=15)
plt.ylabel(r'$f(\alpha)$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 18a: Generating a multifractal image.
# Save the image.
# See Figure 18.1(b).
import numpy as np
import matplotlib.pyplot as plt
from skimage import exposure, io, img_as_uint
p1, p2, p3, p4 = 0.3, 0.4, 0.25, 0.05
p = [[p1, p2], [p3, p4]]
for k in range(1, 9, 1):
M = np.zeros([2 ** (k + 1), 2 ** (k + 1)])
M.tolist()
for i in range(2**k):
for j in range(2**k):
M[i][j] = p1 * p[i][j]
M[i][j + 2**k] = p2 * p[i][j]
M[i + 2**k][j] = p3 * p[i][j]
M[i + 2**k][j + 2**k] = p4 * p[i][j]
p = M
# Plot the multifractal image.
M = exposure.adjust_gamma(M, 0.2)
plt.imshow(M, cmap='gray', interpolation='nearest')
# Save the image as a portable network graphics (png) image.
im = np.array(M, dtype='float64')
im = exposure.rescale_intensity(im, out_range='float')
im = img_as_uint(im)
io.imsave('Multifractal.png', im)
io.show()
# Programs 18d: Counting white pixels in color picture of a raccoon.
# See Figure 18.2.
from scipy import misc
import matplotlib.pyplot as plt
import numpy as np
face = misc.face()
fig1 = plt.figure()
plt.imshow(face)
width, height, _ = face.shape
print('Image dimensions: {}x{}'.format(width, height))
white_pixels = np.zeros((width, height))
def white_pixel_filter(pixel, threshold):
return 1 if all(value > threshold for value in pixel) else 0
for i, row in enumerate(face):
for j, pixel in enumerate(row):
white_pixels[i, j] = white_pixel_filter(pixel, threshold=180)
fig2 = plt.figure()
plt.imshow(white_pixels, cmap='gray')
print('There are {:,} white pixels'.format(int(np.sum(white_pixels))))
plt.show()
Image dimensions: 768x1024 There are 61,253 white pixels
# Program 18c: Statistical Analysis on Microbes.png.
# See Figures 18.3 and 18.4.
import matplotlib.pyplot as plt
from skimage import io
import numpy as np
from skimage.measure import regionprops
from scipy import ndimage
from skimage import feature
microbes_img = io.imread('Microbes.png')
fig1 = plt.figure()
plt.imshow(microbes_img,cmap='gray', interpolation='nearest')
width, height, _ = microbes_img.shape
binary = np.zeros((width, height))
for i, row in enumerate(microbes_img):
for j, pixel in enumerate(row):
if pixel[0] > 80:
binary[i, j] = 1
fig2 = plt.figure()
plt.imshow(binary,cmap='gray')
print('There are {:,} white pixels'.format(int(np.sum(binary))))
blobs = np.where(binary>0.5, 1, 0)
labels, no_objects = ndimage.label(blobs)
props = regionprops(blobs)
print('There are {:,} clusters of cells:'.format(no_objects))
fig3 = plt.figure()
edges=feature.canny(binary,sigma=2,low_threshold=0.5)
plt.imshow(edges,cmap=plt.cm.gray)
fig4 = plt.figure()
labeled_areas = np.bincount(labels.ravel())[1:]
print(labeled_areas)
plt.hist(labeled_areas,bins=no_objects)
plt.xlabel('Area',fontsize=15)
plt.ylabel('Number of clusters',fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
There are 38,895 white pixels There are 106 clusters of cells: [ 73 15 147 255 885 650 197 1065 228 92 99 92 90 39 91 877 691 502 173 366 1081 44 2417 17 225 109 118 75 174 282 632 45 472 289 128 129 13 375 218 97 1159 284 1560 324 1341 346 532 206 114 377 3264 161 263 187 94 133 221 136 214 161 1065 104 92 289 81 92 54 916 451 444 177 1594 1073 179 158 106 181 365 867 838 44 417 336 77 308 383 194 157 48 26 71 180 22 93 218 1024 97 270 181 66 241 50 221 239 62 100]
# Program 18d: Fast Fourier transform (FFT) of a noisy signal.
# See Figure 18.5.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft
Ns = 1000 # Number of sampling points
Fs = 800 # Sampling frequency
T = 1/Fs # Sample time
t = np.linspace(0, Ns*T, Ns)
amp1, amp2 = 0.7, 1
freq1, freq2 = 50, 120
# Sum a 50Hz and 120 Hz sinusoid
x = amp1 * np.sin(2*np.pi * freq1*t) + amp2*np.sin(2*np.pi * freq2*t)
y = x + 0.5*np.random.randn(Ns)
fig1 = plt.figure()
plt.plot(t, y)
plt.xlabel('Time (ms)', fontsize=15)
plt.ylabel('y(t)', fontsize=15)
plt.tick_params(labelsize=15)
fig2 = plt.figure()
yf = fft(y)
xf = np.linspace(0, 1/(2*T), Ns//2)
plt.plot(xf, 2/Ns * np.abs(yf[0:Ns//2]))
plt.xlabel('Frequency (Hz)', fontsize=15)
plt.ylabel('$|Y(f)|$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 18e: Iterative map and power spectra.
# See Figure 18.6.
import matplotlib.pyplot as plt
from scipy.fftpack import fft
import numpy as np
# Parameters
a, b = 1, 0.3 # To get Figures 18.6(e) and (f)
n = 50000
def map_2d(X):
x, y = X
xn = 1 - a*y**2 + b*x
yn = x
return (xn, yn)
X0 = [(1 - b) / 2, (1 - b) / 2]
X, Y = [], []
for i in range(n):
xn, yn = map_2d(X0)
X, Y = X + [xn], Y + [yn]
X0 = [xn, yn]
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(X, Y, color='blue', s=0.05)
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.tick_params(labelsize=15)
fig2 = plt.figure()
f = np.linspace(-1, 1, n)
power = np.abs(fft(X)**2)
power = np.log(power)
plt.plot(f, power)
plt.xlim(0, 1)
plt.xlabel('Frequency (Hz)', fontsize=15)
plt.ylabel('log(Power)', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 18f: Fourier transform of a Lena image.
# See Figure 18.7.
import numpy as np
import skimage.io as io
import pylab
import matplotlib.pyplot as plt
from skimage.color import rgb2gray
lena = rgb2gray(io.imread('lena.jpg'))
fig1 = plt.figure()
plt.imshow(lena, cmap='gray')
fig2 = plt.figure()
# Take the 2-dimensional DFT and centre the frequencies
ftimage = np.fft.fft2(lena)
ftimage = np.fft.fftshift(ftimage)
ftimage = np.abs(ftimage)
fftimage = np.log(ftimage)
fftimage = rgb2gray(fftimage)
pylab.imshow(fftimage, cmap='gray')
plt.show()
<ipython-input-67-a8b3e46b9fe3>:21: FutureWarning: The behavior of rgb2gray will change in scikit-image 0.19. Currently, rgb2gray allows 2D grayscale image to be passed as inputs and leaves them unmodified as outputs. Starting from version 0.19, 2D arrays will be treated as 1D images with 3 channels. fftimage = rgb2gray(fftimage)
# Program 18g: Edge detection on Lena image.
# See Figure 18.8.
import matplotlib.pyplot as plt
import skimage.io as io
from skimage.filters import roberts, sobel
from skimage.color import rgb2gray
lena = rgb2gray(io.imread('lena.jpg'))
edge_roberts = roberts(lena)
edge_sobel = sobel(lena)
fig, ax = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(8, 4))
ax[0].imshow(edge_roberts, cmap=plt.cm.gray)
ax[0].set_title('Roberts Edge Detection')
ax[1].imshow(edge_sobel, cmap=plt.cm.gray)
ax[1].set_title('Sobel Edge Detection')
for a in ax:
a.axis('off')
plt.tight_layout()
plt.show()
# Program 19a: Chaos control in the logistic map.
# Control to period two.
# See Figure 19.3(b).
import matplotlib.pyplot as plt
import numpy as np
# Parameters
mu = 4
k = 0.217
num_iterations = 60
xs, x = [], [0.6]
ns = np.arange(0, num_iterations, 2)
nsc = np.arange(num_iterations, 2*num_iterations, 2)
for n in ns:
x1 = mu*x[n] * (1 - x[n])
x.append(x1)
xs.append([n, x1])
x2 = mu*x1 * (1 - x1)
x.append(x2)
xs.append([n+1, x2])
for n in nsc:
x1 = k*mu*x[n] * (1 - x[n])
x.append(x1)
xs.append([n, x1])
x2 = mu*x1 * (1 - x1)
x.append(x2)
xs.append([n+1, x2])
xs = np.array(xs)
fig, ax = plt.subplots(figsize=(6, 6))
plt.plot(xs[:, 0], xs[:, 1])
plt.plot(xs[:, 0], xs[:, 1], 'ro')
plt.xlabel('n', fontsize=15)
plt.ylabel(r'$x_n$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 19b: Chaos control in the Henon Map.
# See Figure 19.6: Control to period one.
import matplotlib.pyplot as plt
import numpy as np
# Parameters
a, b = 1.2, 0.4
xstar = ystar = 0.8358
k1, k2 = -1.8, 1.2
num_iterations = 199
rs = []
x, y = 0.5, 0.6
ns = np.arange(num_iterations)
nsc = np.arange(num_iterations, 2*num_iterations)
for n in ns:
xn = a + b*y - x**2
yn = x
x, y = xn, yn
r = np.sqrt(x**2 + y**2)
rs.append([n, r])
# Check point is in control region
print(x, y)
for n in nsc:
xn = -k1 * (x - xstar) - k2 * (y - ystar) + a + b*y - x**2
yn = x
x, y = xn, yn
r = np.sqrt(x**2 + y**2)
rs.append([n, r])
rs = np.array(rs)
fig, ax = plt.subplots(figsize=(6,6))
plt.plot(rs[:, 0], rs[:, 1])
plt.plot(rs[:, 0], rs[:, 1], 'ro')
plt.xlabel('n', fontsize=15)
plt.ylabel(r'$r_n^2$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
1.376306895063647 0.41076041951050035
# Program 19c: Synchronization between two Lorenz systems.
# See Figure 19.7(b).
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Constants
sigma = 16
b = 4
r = 45.92
tmax = 100
t = np.arange(0.0, tmax, 0.1)
def two_lorenz_odes(X, t):
x1, x2, x3, y2, y3 = X
dx1 = sigma * (x2 - x1)
dx2 = -x1 * x3 + r*x1 - x2
dx3 = x1 * x2 - b*x3
dy2 = -x1 * y3 + r*x1 - y2
dy3 = x1 * y2 - b*y3
return (dx1, dx2, dx3, dy2, dy3)
y0 = [15, 20, 30, 10, 20]
X = odeint(two_lorenz_odes, y0, t, rtol=1e-6)
x1, x2, x3, y2, y3 = X.T # unpack columns
plt.figure(1)
plt.plot(x3, y3)
plt.xlabel(r'$x_3$', fontsize=15)
plt.ylabel(r'$y_3$', fontsize=15)
plt.show()
# Program 19d: Generalized synchronization.
# See Figure 19.8(a).
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Constants
mu = 5.7
sigma = 16
b = 4
r = 45.92
g = 8 # When g=4, there is no synchronization.
tmax = 100
t = np.arange(0.0, tmax, 0.1)
def rossler_lorenz_odes(X,t):
x1, x2, x3, y1, y2, y3, z1, z2, z3 = X
dx1 = -(x2 + x3)
dx2 = x1 + 0.2*x2
dx3 = 0.2 + x3 * (x1 - mu)
dy1 = sigma * (y2 - y1) - g * (y1 - x1)
dy2 = -y1 * y3 + r*y1 - y2
dy3 = y1 * y2 - b*y3
dz1 = sigma * (z2 - z1) - g * (z1 - x1)
dz2 = -z1*z3 + r*z1 - z2
dz3 = z1*z2 - b*z3
return (dx1, dx2, dx3, dy1, dy2, dy3, dz1, dz2, dz3)
y0 = [2, -10, 44, 30, 10, 20, 31, 11, 22]
X = odeint(rossler_lorenz_odes, y0, t, rtol=1e-6)
x1, x2, x3, y1, y2, y3, x1, z2, z3 = X.T # unpack columns
plt.figure(1)
# Delete first 500 iterates.
plt.plot(y2[500:len(y2)], z2[500:len(z2)])
plt.xlabel(r'$y_2$', fontsize=15)
plt.ylabel(r'$z_2$', fontsize=15)
plt.show()
# Program 20a: The generalized delta learning rule.
# Backpropagation of errors - using the perceptron.
# Training Boston housing data (housing.txt).
# The target is the value of a house (column 13).
# In this case, use 3 attributes (columns 5, 8, and 12).
# See figure 20.7.
import matplotlib.pyplot as plt
import numpy as np
data = np.loadtxt('housing.txt')
rows, columns = data.shape
columns = 4 # Using 4 columns from data in this case
X = data[:, [5, 8, 12]]
t = data[:, 13]
ws1, ws2, ws3, ws4 = [], [], [], []
k = 0
xmean = X.mean(axis=0)
xstd = X.std(axis=0)
ones = np.array([np.ones(rows)])
X = (X - xmean * ones.T) / (xstd * ones.T)
X = np.c_[np.ones(rows), X]
tmean = (max(t) + min(t)) / 2
tstd = (max(t) - min(t)) / 2
t = (t - tmean) / tstd
w = 0.1 * np.random.random(columns)
y1 = np.tanh(X.dot(w))
e1 = t - y1
mse = np.var(e1)
num_epochs = 10 # number of iterations
eta = 0.001
k = 1
for m in range(num_epochs):
for n in range(rows):
yk = np.tanh(X[n, :].dot(w))
err = yk - t[n]
g = X[n, :].T * ((1 - yk**2) * err)
w = w - eta*g
k += 1
ws1.append([k, np.array(w[0]).tolist()])
ws2.append([k, np.array(w[1]).tolist()])
ws3.append([k, np.array(w[2]).tolist()])
ws4.append([k, np.array(w[3]).tolist()])
ws1 = np.array(ws1)
ws2 = np.array(ws2)
ws3 = np.array(ws3)
ws4 = np.array(ws4)
plt.plot(ws1[:, 0], ws1[:, 1], 'k.', markersize=0.1)
plt.plot(ws2[:, 0], ws2[:, 1], 'g.', markersize=0.1)
plt.plot(ws3[:, 0], ws3[:, 1], 'b.', markersize=0.1)
plt.plot(ws4[:, 0], ws4[:, 1], 'r.', markersize=0.1)
plt.xlabel('Number of iterations', fontsize=15)
plt.ylabel('Weights', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 20b: The discrete Hopfield network.
# See Example 5.
from sympy import Matrix, eye
import random
# The fundamental memories:
x1 = [1, 1, 1, 1, 1]
x2 = [1, -1, -1, 1, -1]
x3 = [-1, 1, -1, 1, 1]
X = Matrix([x1, x2, x3])
W = X.T * X / 5 - 3*eye(5) / 5
def hsgn(v, x):
if v > 0:
return 1
elif v == 0:
return x
else:
return -1
L = [0, 1, 2, 3, 4]
n = random.sample(L, len(L))
xinput = [1, -1, -1, 1, 1]
xtest = xinput
for j in range(4):
M = W.row(n[j]) * Matrix(xtest)
xtest[n[j]] = hsgn(M[0], xtest[n[j]])
if xtest == x1:
print('Net has converged to X1')
elif xtest == x2:
print('Net has converged to X2')
elif xtest == x3:
print('Net has converged to X3')
else:
print('Iterate again: May have converged to spurious state')
Net has converged to X2
# Program 20c: Iteration of the minimal chaotic neuromodule.
# See Figure 20.13: Chaotic attractor.
import matplotlib.pyplot as plt
import numpy as np
# Parameters
b1, b2, w11, w21, w12, a = -2, 3, -20, -6, 6, 1
num_iterations = 10000
def neuromodule(X):
x,y=X
xn=b1+w11/(1+np.exp(-a*x))+w12/(1+np.exp(-a*y))
yn=b2+w21/(1+np.exp(-a*x))
return xn,yn
X0 = [0, 2]
X, Y = [], []
for i in range(num_iterations):
xn, yn = neuromodule(X0)
X, Y = X + [xn], Y + [yn]
X0 = [xn, yn]
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(X, Y, color='blue', s=0.1)
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 20d: Bifurcation diagram of the neuromodule.
# See Figure 20.15: Hysteresis in a neuromodule.
from matplotlib import pyplot as plt
import numpy as np
# Parameters
b2, w11, w21, w12, a = 3, 7, 5, -4, 1
start, max = -5, 10
half_N = 1999
N = 2 * half_N + 1
N1 = 1 + half_N
xs_up, xs_down = [], []
x, y = -10, -3
ns_up = np.arange(half_N)
ns_down = np.arange(N1, N)
# Ramp b1 up
for n in ns_up:
b1 = start + n*max / half_N
x = b1 + w11 / (1 + np.exp(-a*x)) + w12 / (1 + np.exp(-a*y))
y = b2+w21 / (1 + np.exp(-a*x))
xn = x
xs_up.append([n, xn])
xs_up = np.array(xs_up)
# Ramp b1 down
for n in ns_down:
b1 = start + 2*max - n*max / half_N
x = b1 + w11 / (1 + np.exp(-a*x)) + w12 / (1 + np.exp(-a*y))
y = b2 + w21 / (1 + np.exp(-a*x))
xn = x
xs_down.append([N-n, xn])
xs_down = np.array(xs_down)
fig, ax = plt.subplots()
xtick_labels = np.linspace(start, max, 7)
ax.set_xticks([(-start + x) / max * N1 for x in xtick_labels])
ax.set_xticklabels(['{:.1f}'.format(xtick) for xtick in xtick_labels])
plt.plot(xs_up[:, 0], xs_up[:, 1], 'r.', markersize=0.1)
plt.plot(xs_down[:, 0], xs_down[:,1], 'b.', markersize=0.1)
plt.xlabel(r'$b_1$', fontsize=15)
plt.ylabel(r'$x_n$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 21a: The Hodgkin-Huxley Equations.
# See Figures 21.2 and 21.3.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Constants
C_m = 1.0 # uF/cm^2
g_Na = 120.0 # mS/cm^2
g_K = 36.0
g_L = 0.3
V_Na = 50.0 # mV
V_K = -77.0
V_L = -54.402
# See equations (21.4)
def alpha_m(V): return 0.1 * (V + 40.0) / (1.0 - np.exp(-0.1 * (V + 40.0)))
def beta_m(V): return 4.0 * np.exp(-0.0556 * (V + 65.0))
def alpha_h(V): return 0.07 * np.exp(-0.05 * (V + 65.0))
def beta_h(V): return 1.0 / (1.0 + np.exp(-0.1 * (V + 35.0)))
def alpha_n(V): return 0.01 * (V + 55.0) / (1.0 - np.exp(-0.1 * (V + 55.0)))
def beta_n(V): return 0.125 * np.exp(-0.0125 * (V + 65))
# See equation (21.2)
def I_Na(V,m,h): return g_Na * m**3 * h * (V - V_Na)
def I_K(V, n): return g_K * n**4 * (V - V_K)
def I_L(V): return g_L * (V - V_L)
# Input current
def Input_current(t): return 10 * (t > 100) - 10 * (t > 200) + 25 * (t > 300)
t = np.arange(0.0, 400.0, 0.1)
# Set up the ODEs, see equations (21.3)
def hodgkin_huxley(X, t):
V, m, h, n = X
dVdt = (Input_current(t) - I_Na(V, m, h) - I_K(V, n) - I_L(V)) / C_m
dmdt = alpha_m(V) * (1.0 - m) - beta_m(V) * m
dhdt = alpha_h(V) * (1.0 - h) - beta_h(V) * h
dndt = alpha_n(V) * (1.0 - n) - beta_n(V) * n
return (dVdt, dmdt, dhdt, dndt)
y0 = [-65, 0.05, 0.6, 0.32]
X = odeint(hodgkin_huxley, y0, t)
V = X[:, 0]
m = X[:, 1]
h = X[:, 2]
n = X[:, 3]
ina = I_Na(V, m, h)
ik = I_K(V, n)
il = I_L(V)
plt.subplots_adjust(hspace = 1)
plt.figure(1)
plt.subplot(5, 1, 1)
plt.title('Hodgkin-Huxley Neuron')
plt.plot(t, V, 'b')
plt.ylabel('V (mV)')
plt.subplot(5, 1, 2)
plt.plot(t, m, 'k')
plt.ylabel('m(V)')
plt.subplot(5, 1, 3)
plt.plot(t, h, 'r')
plt.ylim(0, 1)
plt.ylabel('h(V)')
plt.subplot(5, 1, 4)
plt.plot(t, n, 'g')
plt.ylim(0, 1)
plt.ylabel('n(V)')
plt.subplot(5, 1, 5)
plt.plot(t, Input_current(t), 'm')
plt.ylabel('Input current')
plt.xlabel('Time (ms)')
plt.ylim(-1, 31)
plt.show()
# Program 21b: The Fitzhugh-Nagumo Half-Adder.
# See Figure 21.6.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Input current.
def Input_1(t):
return 1*(t>500)-1*(t>1000)+1*(t>1500)
def Input_2(t):
return 1*(t>1000)
# Constants
theta=0.1;gamma=0.1;epsilon=0.1;
Tmax=2000;
m=-100;c=60;
t=np.arange(0.0, 2000.0, 0.1)
def FN_ODEs(X,t):
u1,v1,u2,v2,u3,v3,u4,v4=X
du1 = -u1*(u1-theta)*(u1-1)-v1+Input_1(t)
dv1 = epsilon*(u1-gamma*v1)
du2 = -u2*(u2-theta)*(u2-1)-v2+Input_2(t)
dv2 = epsilon*(u2-gamma*v2)
du3 = -u3*(u3-theta)*(u3-1)-v3+0.8/(1+np.exp(m*v1+c))+ \
0.8/(1+np.exp(m*v2+c))-1.5/(1+np.exp(m*v4+c))
dv3 = epsilon*(u3-gamma*v3)
du4 = -u4*(u4-theta)*(u4-1)-v4+0.45/(1+np.exp(m*v1+c))+ \
0.45/(1+np.exp(m*v2+c))
dv4 = epsilon*(u4-gamma*v4)
return du1,dv1,du2,dv2,du3,dv3,du4,dv4
X = odeint(FN_ODEs,[0.01,0.01,0.01,0.01,0,0,0,0],t,rtol=1e-6)
u1 = X[:,0];v1 = X[:,1];u2 = X[:,2];v2 = X[:,3]
u3 = X[:,4];v3 = X[:,5];u4 = X[:,6];v4 = X[:,7]
plt.subplots_adjust(hspace = 1)
plt.figure(1)
plt.subplot(4,1,1)
plt.title('Fitzhugh-Nagumo Half-Adder')
plt.plot(t, u1, 'b')
plt.ylim(-1, 1.5)
plt.ylabel('I$_1$')
plt.subplot(4,1,2)
plt.plot(t, u2, 'b')
plt.ylim(-1, 1.5)
plt.ylabel('I$_2$')
plt.subplot(4,1,3)
plt.plot(t, u3, 'g')
plt.ylim(0, 1)
plt.ylim(-1, 1.5)
plt.ylabel('O$_1$')
plt.subplot(4,1,4)
plt.plot(t, u4, 'g')
plt.ylim(-1, 1.5)
plt.ylabel('O$_2$')
plt.xlabel('Time')
plt.show()
# The Fitzhugh-Nagumo Set Reset Flip-Flop.
# The device can be used to store memory.
# Ballistic propagation - only a pulse is required to trigger a switch.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Input current.
def Input_1(t):
return 1*(t>1000)-1*(t>1010) + 1*(t>3000)-1*(t>3010)
def Input_2(t):
return 1*(t>2020)-1*(t>2030) + 1*(t>4000)-1*(t>4010)
# Constants
theta, gamma, epsilon = 0.1, 0.1, 0.1
Tmax=5000
m, c = -100, 60
t=np.arange(0.0, Tmax, 0.1)
w1, w2, x1 = 0.5, 0.9, -1
def FN_ODEs(X,t):
u1,v1,u3,v3,u4,v4,u5,v5,u6,v6=X
# Ic to JJ Neurons
du1 = -u1*(u1-theta)*(u1-1)-v1+1
dv1 = epsilon*(u1-gamma*v1)
# I1 input to JJ Neuron One
du3 = -u3*(u3-theta)*(u3-1)-v3+Input_1(t)
dv3 = epsilon*(u3-gamma*v3)
# I2 input to JJ Neuron Two
du4 = -u4*(u4-theta)*(u4-1)-v4+Input_2(t)
dv4 = epsilon*(u4-gamma*v4)
# Neuron One
du5 = -u5*(u5-theta)*(u5-1)-v5+w1/(1+np.exp(m*v3+c)) \
+x1/(1+np.exp(m*v6+c)) + w2/(1+np.exp(m*v1+c))
dv5 = epsilon*(u5-gamma*v5)
# Neuron Two
du6 = -u6*(u6-theta)*(u6-1)-v6+w1/(1+np.exp(m*v4+c)) \
+x1/(1+np.exp(m*v5+c)) + w2/(1+np.exp(m*v1+c))
dv6 = epsilon*(u6-gamma*v6)
return du1,dv1,du3,dv3,du4,dv4,du5,dv5,du6,dv6
X = odeint(FN_ODEs,[0.01,0.01,0.01,0.01,0.01,0,0,0,0,0],t,rtol=1e-6)
u1 = X[:,0];v1 = X[:,1];u3 = X[:,2];v3 = X[:,3];u4 = X[:,4];v4 = X[:,5]
u5 = X[:,6];v5 = X[:,7];u6 = X[:,8];v6 = X[:,9]
plt.subplots_adjust(hspace = 1)
plt.figure(1)
plt.subplot(5,1,1)
plt.title('Fitzhugh-Nagumo SR flip-flop')
plt.plot(t, u3, 'b')
plt.ylim(-1, 1.5)
plt.ylabel('I$_1$')
plt.subplot(5,1,2)
plt.plot(t, u4, 'b')
plt.ylim(-1, 1.5)
plt.ylabel('I$_2$')
plt.subplot(5,1,3)
plt.plot(t, u5, 'g')
plt.ylim(0, 1)
plt.ylim(-1, 1.5)
plt.ylabel('O$_1$')
plt.subplot(5,1,4)
plt.plot(t, u6, 'g')
plt.ylim(-1, 1.5)
plt.ylabel('O$_2$')
plt.subplot(5,1,5)
plt.plot(t, u1, 'r')
plt.ylim(-1, 1.5)
plt.ylabel('I$_C$')
plt.xlabel('Time')
plt.show()
# Program 21c: Josephson junction (JJ) limit cycle.
# See Figure 21.9.
from matplotlib import pyplot as plt
import numpy as np
from scipy.integrate import odeint
fig = plt.figure()
bj = 1.2
tmax = 100
kappa = 1.4
def jj_ode(x, t):
return [x[1], kappa - bj*x[1] - np.sin(x[0])]
time = np.arange(0, tmax, 0.1)
x0=[0.1,0.1]
xs = odeint(jj_ode, x0, time)
imgplot = plt.plot(np.sin(xs[:, 0]), xs[:, 1], 'r-')
plt.xlabel(r'$\sin(\phi)$', fontsize=15)
plt.ylabel(r'$\Omega$', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()
# Program 21d: Animation of a JJ limit cycle bifurcation.
# These are threshold oscillators, much like biological neurons.
# They oscillate one hundred million times faster than neurons!
# See Figure 21.9.
from matplotlib import pyplot as plt
from matplotlib.animation import ArtistAnimation
import numpy as np
from scipy.integrate import odeint
fig = plt.figure()
myimages = []
bj = 1.2
tmax = 100
def jj_ode(x, t):
return [x[1], kappa - bj*x[1] - np.sin(x[0])]
time = np.arange(0, tmax, 0.1)
x0 = [0.1, 0.1]
for kappa in np.arange(0.1, 2, 0.1):
xs = odeint(jj_ode, x0, time)
imgplot = plt.plot(np.sin(xs[:, 0]), xs[:, 1], 'r-')
myimages.append(imgplot)
anim = ArtistAnimation(fig, myimages, interval=100, blit=False, repeat_delay=100)
plt.show()
from IPython.display import HTML
HTML(anim.to_jshtml())

# Program 21e: Pinched hysteresis in a memristor.
# See Figure 21.12.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Constants
eta, L, Roff, Ron, p, T, w0 = 1.0, 1.0, 70.0, 1.0, 10.0, 20.0, 0.5
t=np.arange(0.0, 40.0, 0.01)
# Set up the ODEs, see equations (21.3)
def memristor(X, t):
w = X
dwdt = ((eta * (1 - (2*w - 1) ** (2*p)) * np.sin(2*np.pi * t/T))
/ (Roff - (Roff - Ron) * w))
return dwdt
X = odeint(memristor, [w0], t, rtol=1e-12)
w = X[:, 0]
plt.plot(np.sin(2*np.pi * t/T), np.sin(2*np.pi * t/T)
/ (Roff - (Roff - Ron) * X[:, 0]), 'b')
plt.xlabel('voltage', fontsize=15)
plt.ylabel('current', fontsize=15)
plt.tick_params(labelsize=15)
plt.show()